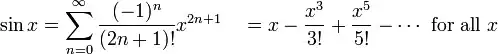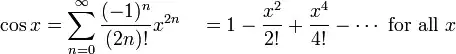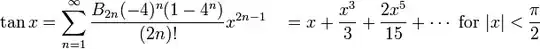Fast transcendent / trigonometric functions for Java

Question

Since the trigonometric functions in java.lang.Math are quite slow: is there a library that does a quick and good approximation? It seems possible to do a calculation several times faster without losing much precision. (On my machine a multiplication takes 1.5ns, and java.lang.Math.sin 46ns to 116ns). Unfortunately there is not yet a way to use the hardware functions.

UPDATE: The functions should be accurate enough, say, for GPS calculations. That means you would need at least 7 decimal digits accuracy, which rules out simple lookup tables. And it should be much faster than java.lang.Math.sin on your basic x86 system. Otherwise there would be no point in it.

For values over pi/4 Java does some expensive computations in addition to the hardware functions. It does so for a good reason, but sometimes you care more about the speed than for last bit accuracy.

Answer 1

Computer Approximations by Hart. Tabulates Chebyshev-economized approximate formulas for a bunch of functions at different precisions.

Edit: Getting my copy off the shelf, it turned out to be a different book that just sounds very similar. Here's a sin function using its tables. (Tested in C since that's handier for me.) I don't know if this will be faster than the Java built-in, but it's guaranteed to be less accurate, at least. :) You may need to range-reduce the argument first; see John Cook's suggestions. The book also has arcsin and arctan.

#include <math.h>
#include <stdio.h>

// Return an approx to sin(pi/2 * x) where -1 <= x <= 1.
// In that range it has a max absolute error of 5e-9
// according to Hastings, Approximations For Digital Computers.
static double xsin (double x) {
  double x2 = x * x;
  return ((((.00015148419 * x2
             - .00467376557) * x2
            + .07968967928) * x2
           - .64596371106) * x2
          + 1.57079631847) * x;
}

int main () {
  double pi = 4 * atan (1);
  printf ("%.10f\n", xsin (0.77));
  printf ("%.10f\n", sin (0.77 * (pi/2)));
  return 0;
}

Answer 2

Here is a collection of low-level tricks for quickly approximating trig functions. There is example code in C which I find hard to follow, but the techniques are just as easily implemented in Java.

Here's my equivalent implementation of invsqrt and atan2 in Java.

I could have done something similar for the other trig functions, but I have not found it necessary as profiling showed that only sqrt and atan/atan2 were major bottlenecks.

public class FastTrig
{
  /** Fast approximation of 1.0 / sqrt(x).
   * See <a href="http://www.beyond3d.com/content/articles/8/">http://www.beyond3d.com/content/articles/8/</a>
   * @param x Positive value to estimate inverse of square root of
   * @return Approximately 1.0 / sqrt(x)
   **/
  public static double
  invSqrt(double x)
  {
    double xhalf = 0.5 * x; 
    long i = Double.doubleToRawLongBits(x);
    i = 0x5FE6EB50C7B537AAL - (i>>1); 
    x = Double.longBitsToDouble(i);
    x = x * (1.5 - xhalf*x*x); 
    return x; 
  }

  /** Approximation of arctangent.
   *  Slightly faster and substantially less accurate than
   *  {@link Math#atan2(double, double)}.
   **/
  public static double fast_atan2(double y, double x)
  {
    double d2 = x*x + y*y;

    // Bail out if d2 is NaN, zero or subnormal
    if (Double.isNaN(d2) ||
        (Double.doubleToRawLongBits(d2) < 0x10000000000000L))
    {
      return Double.NaN;
    }

    // Normalise such that 0.0 <= y <= x
    boolean negY = y < 0.0;
    if (negY) {y = -y;}
    boolean negX = x < 0.0;
    if (negX) {x = -x;}
    boolean steep = y > x;
    if (steep)
    {
      double t = x;
      x = y;
      y = t;
    }

    // Scale to unit circle (0.0 <= y <= x <= 1.0)
    double rinv = invSqrt(d2); // rinv ≅ 1.0 / hypot(x, y)
    x *= rinv; // x ≅ cos θ
    y *= rinv; // y ≅ sin θ, hence θ ≅ asin y

    // Hack: we want: ind = floor(y * 256)
    // We deliberately force truncation by adding floating-point numbers whose
    // exponents differ greatly.  The FPU will right-shift y to match exponents,
    // dropping all but the first 9 significant bits, which become the 9 LSBs
    // of the resulting mantissa.
    // Inspired by a similar piece of C code at
    // http://www.shellandslate.com/computermath101.html
    double yp = FRAC_BIAS + y;
    int ind = (int) Double.doubleToRawLongBits(yp);

    // Find φ (a first approximation of θ) from the LUT
    double φ = ASIN_TAB[ind];
    double cφ = COS_TAB[ind]; // cos(φ)

    // sin(φ) == ind / 256.0
    // Note that sφ is truncated, hence not identical to y.
    double sφ = yp - FRAC_BIAS;
    double sd = y * cφ - x * sφ; // sin(θ-φ) ≡ sinθ cosφ - cosθ sinφ

    // asin(sd) ≅ sd + ⅙sd³ (from first 2 terms of Maclaurin series)
    double d = (6.0 + sd * sd) * sd * ONE_SIXTH;
    double θ = φ + d;

    // Translate back to correct octant
    if (steep) { θ = Math.PI * 0.5 - θ; }
    if (negX) { θ = Math.PI - θ; }
    if (negY) { θ = -θ; }

    return θ;
  }

  private static final double ONE_SIXTH = 1.0 / 6.0;
  private static final int FRAC_EXP = 8; // LUT precision == 2 ** -8 == 1/256
  private static final int LUT_SIZE = (1 << FRAC_EXP) + 1;
  private static final double FRAC_BIAS =
    Double.longBitsToDouble((0x433L - FRAC_EXP) << 52);
  private static final double[] ASIN_TAB = new double[LUT_SIZE];
  private static final double[] COS_TAB = new double[LUT_SIZE];

  static
  {
    /* Populate trig tables */
    for (int ind = 0; ind < LUT_SIZE; ++ ind)
    {
      double v = ind / (double) (1 << FRAC_EXP);
      double asinv = Math.asin(v);
      COS_TAB[ind] = Math.cos(asinv);
      ASIN_TAB[ind] = asinv;
    }
  }
}

Answer 3

That might make it : http://sourceforge.net/projects/jafama/

Answer 4

On the x86 the java.lang.Math sin and cos functions do not directly call the hardware functions because Intel didn't always do such a good job implimenting them. There is a nice explanation in bug #4857011.

http://bugs.sun.com/bugdatabase/view_bug.do?bug_id=4857011

You might want to think hard about an inexact result. It's amusing how often I spend time finding this in others code.

"But the comment says Sin..."

Answer 5

I'm surprised that the built-in Java functions would be so slow. Surely the JVM is calling the native trig functions on your CPU, not implementing the algorithms in Java. Are you certain your bottleneck is calls to trig functions and not some surrounding code? Maybe some memory allocations?

Could you rewrite in C++ the part of your code that does the math? Just calling C++ code to compute trig functions probably wouldn't speed things up, but moving some context too, like an outer loop, to C++ might speed things up.

If you must roll your own trig functions, don't use Taylor series alone. The CORDIC algorithms are much faster unless your argument is very small. You could use CORDIC to get started, then polish the result with a short Taylor series. See this StackOverflow question on how to implement trig functions.

Answer 6

You could pre-store your sin and cos in an array if you only need some approximate values. For example, if you want to store the values from 0° to 360°:

double sin[]=new double[360];
for(int i=0;i< sin.length;++i) sin[i]=Math.sin(i/180.0*Math.PI):

you then use this array using degrees/integers instead of radians/double.

Answer 7

I haven't heard of any libs, probably because it's rare enough to see trig heavy Java apps. It's also easy enough to roll your own with JNI (same precision, better performance), numerical methods (variable precision / performance ) or a simple approximation table.

As with any optimization, best to test that these functions are actually a bottleneck before bothering to reinvent the wheel.

Answer 8

Trigonometric functions are the classical example for a lookup table. See the excellent

• Lookup table article at wikipedia

If you're searching a library for J2ME you can try:

• the Fixed Point Integer Math Library MathFP

Answer 9

The java.lang.Math functions call the hardware functions. There should be simple appromiations you can make but they won't be as accurate.

On my labtop, sin and cos takes about 144 ns.

Answer 10

In the sin/cos test I was performing for integers zero to one million. I assume that 144 ns is not fast enough for you.

Do you have a specific requirement for the speed you need?

Can you qualify your requirement in terms of time per operation which is satisfactory?

Answer 11

Check out Apache Commons Math package if you want to use existing stuff.

If performance is really of the essence, then you can go about implementing these functions yourself using standard math methods - Taylor/Maclaurin series', specifically.

For example, here are several Taylor series expansions that might be useful (taken from wikipedia):

Answer 12

Could you elaborate on what you need to do if these routines are too slow. You might be able to do some coordinate transformations ahead of time some way or another.