Gaussian kernels are separable, which means you can do a horizontal pass first, then a vertical pass (or the other way around). That turns O(N^2) into O(2N). That works for all separable filters, not just for blur (not all filters are separable, but many are, and some are "as good as").
Or,in the particular case of a blur filter (Gauss or not), which are all kind of "weighted sums", you can take advantage of texture interpolation, which may be faster for small kernel sizes (but definitively not for large kernel sizes).
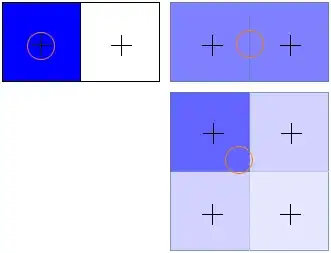
EDIT: image for the "linear interpolation" method
EDIT (as requested by Jerry Coffin) to summarize the comments:
In the "texture filter" method, linear interpolation will produce a weighted sum of adjacent texels according to the inverse distance from the sample location to the texel center. This is done by the texturing hardware, for free. That way, 16 pixels can be summed in 4 fetches. Texture filtering can be exploited in addition to separating the kernel.
In the example image, on the top left, your sample (the circle) hits the center of a texel. What you get is the same as "nearest" filtering, you get that texel's value. On the top right, you are in the middle between two texels, what you get is the 50/50 average between them (pictured by the lighter shader of blue). On the bottom right, you sample in between 4 texels, but somewhat closer to the top left one. That gives you a weighted average of all 4, but with the weight biased towards the top left one (darkest shade of blue).
The following suggestions are courtesy of datenwolf (see below):
"Another methods I'd like suggest is operating in fourier space, where convolution turns into a simple product of fourier transformed signal and fourier transformed kernel. Although the fourier transform on the GPU itself is quite tedious to implement, at least using OpenGL shaders. But it's quite easy done in OpenCL. Actually I implement such things using OpenCL, now, a lot of image processing in my 3D engine happens in OpenCL.
OpenCL has been specifically designed for running on GPUs. A Fast Fourier Transform is actually the piece of example code on Wikipedia's OpenCL article: en.wikipedia.org/wiki/OpenCL and yes the performance gain is tremendous. A FFT executes with at most O(n log n), the reverse the same. The filter kernel fourier representation can be precomputed. The way is FFT -> multiply with kernel -> IFFT, which boils down to O(n + 2n log n) operations. Take note the the actual convolution is just O(n) there.
In the case of a separable, finite convolution like a gaussian blur the separation solution will outperform the fourier method. But in case of generalized, possible non-separable kernels the fourier methods is probably the fastest method available.
OpenCL integrates nicely with OpenGL, e.g. you can use OpenGL buffers (textures and vertex) for both input and ouput of OpenCL programs."
