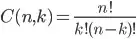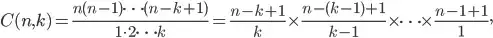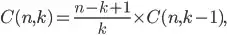Recursive function for finding combinations without hitting the built-in limit in python

Question

I have put together a function for finding combinations using recursion without hitting the built in limit in python. For example you could calculate: choose(1000, 500). This is how it looks right now:

def choose(n, k):
    if not k: 
    return 1 .
elif n < k: 
    return 0
else:
    return ((n + 1 - k) / k) * choose(n, k - 1)

It works exactly how I want it to work. If k is 0 then return 1 and if n is less then k then return 0 (this is according to the mathematical definitions I found on wikipedia). However, the problem is that I don't quite understand the last row (found it when I was browsing the web). Before the last row I'm using at the moment, this was the last row I had in the function:

return choose(n-1,k-1) + choose(n-1, k)

Which I also found on wikipedia (though I don't think I understand this one a 100% as well). But it would always result in an error because of the built in limitation in python, whereas the new line I'm using does not result in such an error. I understand that the new line works much more efficient with the program, because we for example don't split it up to two subproblems.

So again.. what I'm asking is if there are any kind souls out there that could explain (in an understandable manner) how this line of code works in the function:

return ((n + 1 - k) / k) * choose(n, k - 1)

I wouldn't use recursion for this, unless it's specifically an exercise in learning recursion. You can do it with a simple loop, or the factorial function. See https://stackoverflow.com/a/26561091/4014959 — PM 2Ring, Sep 22 '18 at 22:14

score 0 · Accepted Answer · answered Sep 22 '18 at 22:21

You would first need to know how combination C(n, k) is defined. The formula for C(n, k) is:

or, equivalently:

which can be reformed into a recursive expression:

which is what you implemented.

For the second implemention, this is the Pascal's formula. A recursive implementation would be very slow (and potentionly stack overflow, yes). A more efficient implementation would be to store each C(n, k) in a two-dimensional array to calculate each value in order.

Olivier Melançon · Answer 2 · 2018-09-22T22:28:11.693

Spoiler: the bottom line will be that you should use the closed form n! / (k! (n - k)!).

In many other languages, the solution would be to make your function tail-recursive, although Python does not support this kind of optimization. Thus implementing recursive solution is simply not the best option.

You could increase the maximal recursion depth with sys.setrecursionlimit, but this is not optimal.

An improvement would be to compute n-choose-k with iteration.

def choose(n, k):
    if n < k:
        return 0

    ans = 1
    while k > 0:
        ans *= (n + 1 - k) / k
        k -= 1

    return ans

Although, the above will accumulate an error due to float arithmetic. The very best approach is thus to use the closed form of n-choose-k.

from math import factorial

def choose(n, k):
    return factorial(n) / (factorial(k) * factorial(n - k))

Recursive function for finding combinations without hitting the built-in limit in python

2 Answers2