I have a question about my own project for testing reinforcement learning technique. First let me explain you the purpose. I have an agent which can take 4 actions during 8 steps. At the end of this eight steps, the agent can be in 5 possible victory states. The goal is to find the minimum cost. To access of this 5 victories (with different cost value: 50, 50, 0, 40, 60), the agent don't take the same path (like a graph). The blue states are the fail states (sorry for quality) and the episode is stopped.
The real good path is: DCCBBAD
Now my question, I don't understand why in SARSA & Q-Learning (mainly in Q learning), the agent find a path but not the optimal one after 100 000 iterations (always: DACBBAD/DACBBCD). Sometime when I compute again, the agent falls in the good path (DCCBBAD). So I would like to understand why sometime the agent find it and why sometime not. And there is a way to look at in order to stabilize my agent?
Thank you a lot,
Tanguy
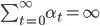
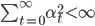
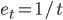 , too.
To hit 2 and 3, you must ensure you take care of 1, so that you collect infinite learning rates, but also pick your learning rate so that its square is finite. That basically means =< 1. If your environment is deterministic you should try 1. Deterministic environment here that means when taking an action
, too.
To hit 2 and 3, you must ensure you take care of 1, so that you collect infinite learning rates, but also pick your learning rate so that its square is finite. That basically means =< 1. If your environment is deterministic you should try 1. Deterministic environment here that means when taking an action