Problem
I created a set of polygons based on bag of plane intersection.
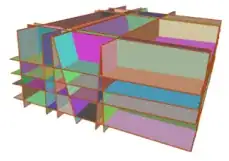
Now I try to create the following manifold by combinatorial optimization.
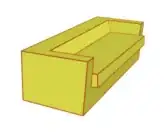
- Manifold constraint each edge in the final model should be incident to two polygons.
- Optimize weight each polygon has a confidence weight, the model should optimize towards highest overal confidence
- Optimize simplicity Optimize towards less corners (more polygons in the same plane)
Attempt
The idea was to use python-constraint to generate possible solutions and select the best fitting by optimization of some weights on each polygon with scipy.optimize.
However, tried the following with python-constraint and it is not able to generate solutions.
import constraint
problem = constraint.Problem()
problem.addVariables(range(len(polygons)), [True, False])
for idx, polygon in enumerate(polygons):
edge_adjacent_polygons = [polygon[a][b]['polygon'] for a, b in polygon.edges()]
if all([len(adjacent_polygons) > 2 for adjacent_polygons in edge_adjacent_polygons]):
for adjacent_polygons in edge_adjacent_polygons:
problem.addConstraint(lambda *adjacent_polygons: sum(adjacent_polygons) == 2, adjacent_polygons)
elif any([len(adjacent_polygons) == 2 for adjacent_polygons in edge_adjacent_polygons]) & \
all([len(adjacent_polygons) >= 2 for adjacent_polygons in edge_adjacent_polygons]):
problem.addConstraint(lambda idx: idx == True, [idx])
else:
problem.addConstraint(lambda idx: idx == False, [idx])
Other ideas I had were to model this as a graph optimization problem in NetworkX and using something like min_weighted_vertex_cover. Or using the jMetalPy library, however it is unclear to me how to model this problem in these approaches.
Question
I understand this problem combines non-linear optimization and a combinatorial satisfaction problem. My most important questions are;
- is my approach correct or overcomplicated?
- does a tool exist to model such a problem?
The original problem (and images) are from a paper I try to replicate https://repository.kaust.edu.sa/handle/10754/627151. In the paper the proprietary Gurobi solver is used. I cannot use this solver due to license.