I've got a weird problem I've been trying to solve for a few days and I'm wondering if someone can help me out.
I have the following pieces of information:
- A standard PSR (position, scale, and rotation) matrix
- An origin point in 3D space defining the starting point of a ray
- A normal vector in 3D space relative to #2 that defines the ray direction
- A target point in 3D space
The ray origin and normal can be located anywhere in 3D space, but they must be parented to the matrix described in #1 (which itself can have any initial rotation and/or position within 3D space).
What I need to do is to calculate the rotation of the parent matrix to ensure that the ray origin and ray direction are aligned in such a way that the ray is guaranteed to intersect with the target point, preferably using an up vector for alignment if there is more than one possible solution.
Is there any straightforward way to calculate this?
EDIT:
Here's some pictures that show exactly what I'm trying to do. Apologies for the confusion!
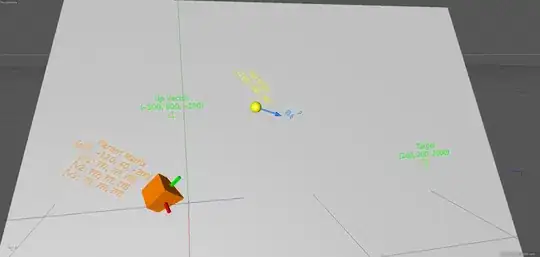
In this picture, the orange cube represents the parent matrix (with no rotation), the yellow sphere represents the ray origin, and the blue arrow represents the ray direction. There's also an up vector and target point.
I need to rotate the matrix the ray origin and direction are parented to so that the ray points directly at the target object, with the ray origin falling on a 2D plane defined by the parent matrix position, target point, and up vector.
Here's a third example showing how the ray direction now points directly at the target point.
And finally here's another picture that roughly shows how the entire thing needs to be aligned with the up vector.
The primary problem here is that nothing is constant- the parent matrix offset (read: position) could change, or the ray origin and direction could change. The target point will also move around, as can the up vector- meaning that I need to figure out how to realign everything as the objects shift around in 3D space.