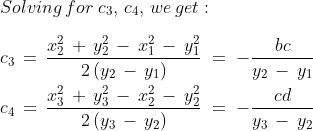When searching for code to calculate the circle out of 3 points it leads me to this code:
def circleRadius(b, c, d):
temp = c[0]**2 + c[1]**2
bc = (b[0]**2 + b[1]**2 - temp) / 2
cd = (temp - d[0]**2 - d[1]**2) / 2
det = (b[0] - c[0]) * (c[1] - d[1]) - (c[0] - d[0]) * (b[1] - c[1])
if abs(det) < 1.0e-10:
return None
# Center of circle
cx = (bc*(c[1] - d[1]) - cd*(b[1] - c[1])) / det
cy = ((b[0] - c[0]) * cd - (c[0] - d[0]) * bc) / det
radius = ((cx - b[0])**2 + (cy - b[1])**2)**.5
return radius
Based on Stackoverflow and Dr.Math. The code works perfectly, but I don't understand how the code fits to the explanation given at Dr.Math.
Can anyone help me to understand why the code is working and what substeps are implemented in the variables?
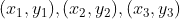 be the points on the triangle. [b is point 1, c is point 2, and d is point 3]
be the points on the triangle. [b is point 1, c is point 2, and d is point 3]