Generate a random number with max, min and mean(average) in Java

Question

I need to generate random numbers with following properties.

Min should be 200

Max should be 20000

Average(mean) is 500.

Optional: 75th percentile to be 5000

Definitely it is not uniform distribution, nor gaussian. I need to give some left skewness.

Answer 1

Java Random probably won't work because it only gives you normal(gaussian) distributions.

What you're probably looking for is an f distribution (see below). You can probably use the distlib library here and choose the f distribution. You can use the random method to get your random number.

Answer 2

Say X is your target variable, lets normalize the range by doing Y=(X-200)/(20000-200). So now you want some Y random variable that takes values in [0,1] with mean (500-200)/(20000-200)=1/66.

You have many options, the most natural one seems to me a Beta distribution, Y ~ Beta(a,b) with a/(a+b) = 1/66 - you have an extra degree of freedom, which you can choose either to fit the last quartile requirement.

After that, you simply return X as Y*(20000-200)+200

To generate a Beta random variable, you can use Apache Commons or see here.

Answer 3

This may not be the answer you're looking for, but the specific case with 3 uniform distributions:

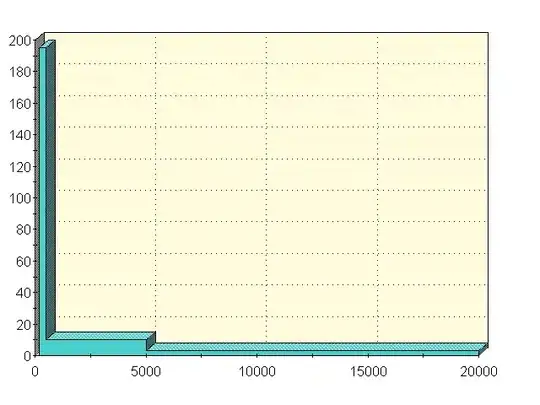(Ignore the numbers on the left, but it is to scale!)

public int generate() {
  if(random(0, 65) == 0) {
    // 50-100 percentile

    if(random(1, 13) > 3) {
      // 50-75 percentile
      return random(500, 5000);
    } else {
      // 75-100 percentile
      return random(5000, 20000);
    }

  } else {
    // 0-50 percentile
    return random(200, 500);
  }
}

How I got the numbers

First, the area under the curve is equal between 200-500 and 500-20000. This means that the height relationship is 300 * leftHeight == 19500 * rightHeight making leftHeight == 65 * rightHeight

This gives us a 1/66 chance to choose right, and a 65/66 chance to choose left.

I then made the same calculation for the 75th percentile, except the ratio was 500-5000 chance == 5000-20000 chance * 10 / 3. Again, this means we have a 10/13 chance to be in 50-75 percentile, and a 3/13 chance to be in 75-100.

Kudos to @Stas - I am using his 'inclusive random' function.

And yes, I realise my numbers are wrong as this method works with discrete numbers, and my calculations were continuous. It would be good if someone could correct my border cases.

Answer 4

You can have a function f working on [0;1] such as

Integral(f(x)dx) on [0;1] = 500
f(0) = 200
f(0.75) = 5000
f(1) = 20000

I guess a function of the form

f(x) = a*exp(x) + b*x + c

could be a solution, you just have to solve the related system.

Then, you do f(uniform_random(0,1)) and there you are !

Answer 5

Your question is vague as there are numerous random distributions with a given minimum, maximum, and mean.

Indeed, one solution among many is to choose max with probability (mean-min)/(max-min) and min otherwise. That is, this solution generates one of only two numbers — the minimum and the maximum.

The following is another solution.

The PERT distribution (or beta-PERT distribution) is designed to take a minimum and maximum and estimated mode. It's a "smoothed-out" version of the triangular distribution, and generating a random variate from that distribution can be implemented as follows:

startpt + (endpt - startpt) * 
     BetaDist(1.0 + (midpt - startpt) * shape / (endpt - startpt), 
          1.0 + (endpt - midpt) * shape / (endpt - startpt))

where—

• startpt is the minimum,
• midpt is the mode (not necessarily average or mean),
• endpt is the maximum,
• shape is a number 0 or greater, but usually 4, and
• BetaDist(X, Y) returns a random variate from the beta distribution with parameters X and Y.

Given a known mean (mean), midpt can be calculated by:

3 * mean / 2 - (startpt + endpt) / 4