Calculating confidence Interval around a Linear Regression Line

Question

I am trying to calculate confidence interval around a linear regression line. For my research, I have to know the equation of upper and lower 95% confidence interval curves around the regression line.

The x and y of my data is... x = [0.18 0.19 0.02 0.27 0.21 0.14 0.30 0.37 0.16 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.03 0.05 0.00]

and y = [115.74 212.91 114.30 182.58 92.71 235.60 160.05 230.11 89.60 31.29 77.27 41.42 121.40 37.42 42.52 45.71 89.13 94.68 94.51 91.64 44.39 125.87 67.09]

First, I used this code to create 95% confidence curves:

model1 <- lm(y ~ x, data=SSY)
newx <- seq(0.0000, 0.45000, by=0.01)
conf_interval <- predict(model1, newdata=data.frame(x=newx), interval="confidence",
                     level = 0.95)

I've got beautiful graph showing 95% confidence curves with regression line but no equations for the curves were displayed.

So, next, I tried to calculate the confidence interval manually using this equation:

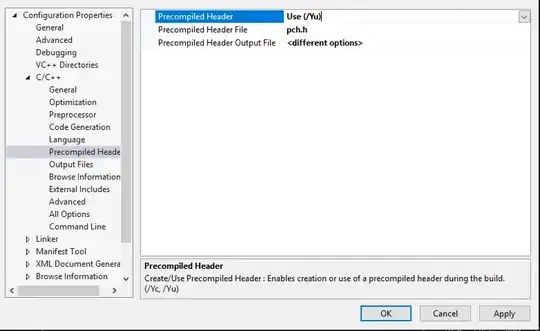
Where the (s.e.) is defined as standard error of the regression line multipled by the standard error of the estimate at xk:

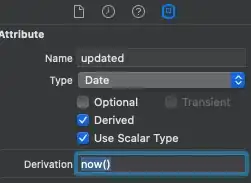
# Extract fitted coefficients from model object
b0 <- model1$coefficients[1]
b1 <- model1$coefficients[2]
y <- SSY$y
x <- SSY$x

#Critical t-value
t.val <- qt(0.975, 21)


# Fit a new linear model that extends past the given data points (for plotting)
x_new <- seq(0.0000, 0.45000, by=0.01)
y.fit <- b1 * x_new + b0

se <- sqrt(sum((y - y.fit)^2) / (21)) * sqrt(1 / 21 + (x_new - mean(x))^2 / sum((x_new - mean(x))^2))

# Warnings of mismatched lengths are suppressed
slope.upper <- suppressWarnings(y.fit + t.val * se)
slope.lower <- suppressWarnings(y.fit - t.val * se)

However, the results from predict() function and manual computation are different:

1. Predict() function:

fit: 73.5833 77.46624 81.34918 ... 248.31552

lwr: 50.97287 55.75834 60.46065 ... 187.02017

upr: 96.19373 99.17413 102.2377 ... 309.61086

2. Manual computation:

fit: 73.5833 77.46624 81.34918 ... 248.31552

lwr: 0.61771 5.14366 9.59238 ... 134.71490

upr: 146.5489 149.7888 153.1060 ... 361.9161

Is there anybody know what's wrong?

Thank you!