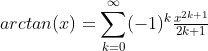What should I change so that my arctan(x) approximation can display x=1 and x=-1 properly?

Question

One of my C assignments was it to write an approximation of arctan(x) in the language C. The equation which I should base it on is

arctan(x)=\sum {k=0}^{\infty }(-1)^{k} \tfrac{x^{2k+1}}{2k+1}

In addition x is only defined as -1<=x<=1.

Here is my code.

#include <stdio.h>
#include <math.h>


double main(void) {

    double x=1;
    double k;
    double sum;
    double sum_old;
    int count;

    double pw(double y, double n) {
        double i;
        double number = 1;

        for (i = 0; i < n; i++) {
            number *= y;
        }
        return(number);
    }

    double fc (double y) {
        double i;
        double number = 1;

        for (i = 1; i <= y; i++){
            number *= i;
        }
        return(number);
    }

    if(x >= (-1) && x <= 1) {
        for(k=0; sum!=sum_old; k++) {
            sum_old = sum;
            sum += pw((-1), k) * pw(x, (2*k) + 1)/((2*k) + 1);
            count++;

            printf("%d || %.17lf\n", count, sum);
        } 



    printf("My result is: %.17lf\n",sum);
    printf("atan(%f) is: %.17f\n", x, atan(x));
    printf("My result minus atan(x) = %.17lf\n", sum - atan(x));
    } else {
        printf("x is not defined. Please choose an x in the intervall [-1, 1]\n");
        }



return 0;
}

It seemingly works fine with every value, except value 1 and -1. If x=1, then the output ends with:

...
7207 || 0.78543285189457468
7208 || 0.78536

Whereas the output should look more like this. In this case x=0.5.

25 || 0.46364760900080587
26 || 0.46364760900080587
My result is: 0.46364760900080587
atan(0.500000) is: 0.46364760900080609
My result minus atan(x) atan(x) = -0.00000000000000022

How can I improve my code so that it can run with x=1 and x=-1.

Thanks in advance.

PS: I use my own created pw() function instead of pow(), because I wanted to bybass the restriction of not using pow() as we didn't had that in our lectures yet.

PPS: I'd appreciate any advice as to how to improve my code.

Answer 1

In each iteration, you add (-1)^k • x^2k+1 / (2k+1), and you stop when there is no change to the sum.

If this were calculated with ideal arithmetic (exact, infinitely precise arithmetic), it would never stop for non-zero x, since you are always changing the sum. When calculating with fixed-precision arithmetic, it stops when the term is so small it does not change the sum because of the limited precision.

When |x| is less than one by any significant amount, this comes quickly because x^2k+1 gets smaller. When |x| is one, the term becomes just 1 / (2k+1), which gets smaller very slowly. Not until k is around 2⁵³ would the sum stop changing.

You might consider changing your stopping condition to be when sum has not changed from sum_old very much rather than when it has not changed at all.

Answer 2

if(x >= (-1) && x <= 1) {
    for(k=0; sum!=sum_old; k++) {
        sum_old = sum;
        sum += pw((-1), k) * pw(x, (2*k) + 1)/((2*k) + 1);
        count++;

        printf("%d || %.17lf\n", count, sum);
    } 

Comparing doubles can be tricky. The conventional way to compare doubles is to test within epsilon. There should be an epsilon value defined somewhere, but for your purposes how many digits are enough to approximate? If you only need like 3 or 4 digits you can instead have

#define EPSILON 0.0001 //make this however precise you need to approximate.

if(x >= (-1) && x <= 1) {
    for(k=0; fabs(sum - sum_old) > EPSILON; k++) {
        sum_old = sum;
        sum += pw((-1), k) * pw(x, (2*k) + 1)/((2*k) + 1);
        count++;

        printf("%d || %.17lf\n", count, sum);
    } 

If the issue is that -1,1 iterate too many times either reduce the precision or increase the step per iteration. I am not sure that is what you're asking though, please clarify.

Answer 3

I think the cause of this is for a mathematical reason rather than a programming one.

Away from the little mistakes and adjustments that you should do to your code, putting x = 1 in the infinite series of arctan, is a boundary condition: In this series, we add a negative value to a positive value then a negative value. This means the sum will be increasing, decreasing, increasing, ... and this will make some difference each iteration. This difference will be smaller until the preciseness of double won't catch it, so the program will stop and give us the value.

But in the sum equation. When we set z = 1 and n goes from 0 to ∞, this will make this term (-1^n) equal to 1 in one time and -1 in the next iteration. Also, the value of the z-term will be one and the denominator value when n approaches infinity will = ∞ .

So the sum several iterations will be like +1/∞ -1/∞ +1/∞ -1/∞ ... (where ∞ here represents a big number). That way the series will not reach a specific number. This is because z = 1 is a boundary in this equation. And that is causing infinite iterations in your solution without reaching a number.

If you need to calculate arctan(1) I think you should use this formula:

All formulas are from this Wikipedia article.

Answer 4

Here is some modifications that make your code more compact and has less errors:

#include <stdio.h>
#include <math.h>

#define x 0.5               //here x is much easier to change

double pw(double, double);      //declaration of the function should be done

int main() {                    //the default return type of main is int.

    double k;
    double sum = 0 ;                //you should initiate your variables.
    double sum_old = 1 ;            //=1 only to pass the for condition first time.
                                    //you don't need to define counter here
    if(x < -1 || x > 1){
        printf("x is not defined. Please choose an x in the interval [-1, 1]\n");
        return 0;
    }
    for(k=0; sum!=sum_old; k++) {
        sum_old = sum;
        sum += pw((-1), k) * pw(x, (2*k) + 1)/((2*k) + 1);
        printf("%.0f || %.17lf\n", k, sum);
    }

    printf("My result is: %.17lf\n",sum);
    printf("atan(%f) is: %.17f\n", x, atan(x));
    printf("My result minus atan(x) = %.17lf\n", sum - atan(x));

return 0;
}

double pw(double y, double n) {         //functions should be declared out of the main function
    double i;
    double number = 1;

    for (i = 0; i < n; i++) {
        number *= y;
    }
    return(number);
}

double fc (double y) {
    double i;
    double number = 1;

    for (i = 1; i <= y; i++){
        number *= i;
    }
    return(number);
}