Why is a sudden twist/roll introduced when rotating a quaternion in certain directions?

Question

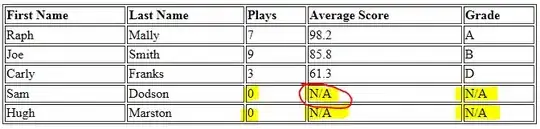
Scenario

Given a normalised quaternion, A_q, and a normalised direction vector, B_v, we calculate a new rotation, C_q, that will rotate A_q to "face" in the direction of B_v. To clarify, let D_q = C_q * A_q, such that (1,0,0) rotated by D_q will be equal to B_v.

N.B. For notational convenience, from now on we will refer to (1,0,0) rotated by any quaternion as that quaternion's symbol with the suffix _v, i.e. (1,0,0) rotated by A_q becomes A_v.

Demonstration

I have implemented such a scenario here (interactive), with source here, and have attached a gif below too.

My Problem

My problem is that when A_v and B_v are close to opposite (or seemingly approaching anti-parallel), D_q exhibits a sudden twist/roll, which is undesirable. The image above demonstrates this.

The code in question

It is in UE4's C++ API, but it should be language/framework agnostic enough to parse:

FTransform UMWEUtil::FindNewRotation(FTransform A_t, FVector B_v)
{
    FQuat A_q = A_t.GetRotation();
    FVector A_v = A_q.GetForwardVector();

    A_v.Normalize();
    B_v.Normalize();

    FVector AxisOfRotation = FVector::CrossProduct(A_v, B_v).GetSafeNormal();
    float Rads = FMath::Acos(FVector::DotProduct(A_v, B_v));
    FQuat C_q(AxisOfRotation, Rads);

    FQuat D_q = C_q * A_q;

    return FTransform(D_q);
}

My questions

1. Why does this sudden roll/twist artifact occur?
2. I am guessing it is because of cross product A_v X B_v changing hemispheres. But then, why does it only occur once, not twice (the cross product, A_v X B_v is seen transitioning hemispheres twice in a full rotation)?
3. Finally, the solution I have come up with is to decompose D_q into swing/twist quaternions and only use the swing quaternion (thus, removing the sudden twist). However, this feels like a band-aid due to my lack of understanding of the problem, is there a different solution that will result in a smooth transition?

My solution (maybe unnecessary?)

FTransform UMWEUtil::FindNewRotation2(FTransform A_t, FVector B_v)
{
    FQuat A_q = A_t.GetRotation();
    FVector A_v = A_q.GetForwardVector();

    A_v.Normalize();
    B_v.Normalize();

    FVector AxisOfRotation = FVector::CrossProduct(A_v, B_v).GetSafeNormal();
    float Rads = FMath::Acos(FVector::DotProduct(A_v, B_v));
    FQuat C_q(AxisOfRotation, Rads);

    FQuat D_q = C_q * A_q;

    FQuat OutSwing;
    FQuat OutTwist;

    D_q.ToSwingTwist(FVector::ForwardVector, OutSwing, OutTwist);

    return FTransform(OutSwing);
}