I don't really follow how they came up with the derivative equation. Could somebody please explain in some details or even a link to somewhere with sufficient math explanation?
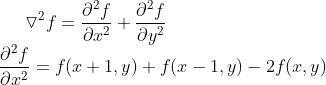
Laplacian filter looks like
I don't really follow how they came up with the derivative equation. Could somebody please explain in some details or even a link to somewhere with sufficient math explanation?
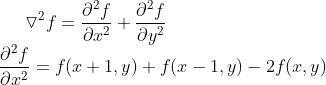
Laplacian filter looks like
Monsieur Laplace came up with this equation. This is simply the definition of the Laplace operator: the sum of second order derivatives (you can also see it as the trace of the Hessian matrix).
The second equation you show is the finite difference approximation to a second derivative. It is the simplest approximation you can make for discrete (sampled) data. The derivative is defined as the slope (equation from Wikipedia):
In a discrete grid, the smallest h is 1. Thus the derivative is f(x+1)-f(x). This derivative, because it uses the pixel at x and the one to the right, introduces a half-pixel shift (i.e. you compute the slope in between these two pixels). To get to the 2nd order derivative, simply compute the derivative on the result of the derivative:
f'(x) = f(x+1) - f(x)
f'(x+1) = f(x+2) - f(x+1)
f"(x) = f'(x+1) - f'(x)
= f(x+2) - f(x+1) - f(x+1) + f(x)
= f(x+2) - 2*f(x+1) + f(x)
Because each derivative introduces a half-pixel shift, the 2nd order derivative ends up with a 1-pixel shift. So we can shift the output left by one pixel, leading to no bias. This leads to the sequence f(x+1)-2*f(x)+f(x-1).
Computing this 2nd order derivative is the same as convolving with a filter [1,-2,1].
Applying this filter, and also its transposed, and adding the results, is equivalent to convolving with the kernel
[ 0, 1, 0 [ 0, 0, 0 [ 0, 1, 0
1,-4, 1 = 1,-2, 1 + 0,-2, 0
0, 1, 0 ] 0, 0, 0 ] 0, 1, 0 ]