This turned out to be much more complicated than I at first anticipated. The way I solved it was to first rotate the object into a frontal view (in terms of the Axes3D elev and azim angles), projected it onto the y-z-plane, compute the 2D outline, re-add the third dimension and then rotating the now 3D outline back into the current view.
The rotation part can be accomplished with simple matrix operation, one only has to take care that the x, y, and z axes may be stretched and need to be un-stretched before rotation.
The projection part was a bit tricky, as I don't know of any clever way to find the outer points of such a large collection of points. I therefore solved it by calculating the projection of each simplex separately, compute their 2D convex hulls (using scipy), convert them into shapely polygons, and finally compute the union of all these polygons. I then added back the missing x-coordinate and rotated the entire thing back into the current view.
By default, Axes3D objects use perspective, causes the actual outline of the object to not align perfectly with the computed projection. This can be avoided by using an orthogonal view (set with ax.set_proj_type('ortho')).
Finally, once the image is rotated, the outline/projection needs to be updated. I therefore added the entire function to the event queue following this example.
Please ask if there are any further questions.
from mpl_toolkits.mplot3d import Axes3D
from mpl_toolkits.mplot3d.art3d import Poly3DCollection, Line3DCollection
from matplotlib import pyplot as plt
import numpy as np
from shapely.geometry import Polygon
from scipy.spatial import ConvexHull
from scipy.spatial import Delaunay
##the figure
fig, ax = plt.subplots(subplot_kw=dict(projection='3d'))
##generating some random points:
points = np.random.rand(50,3)
xmin,xmax = 0,100
ymin,ymax = -10,10
zmin,zmax = -20,20
points[:,1] = (points[:,1]*(ymax-ymin)+ymin) * np.sin(points[:,0]*np.pi)
points[:,2] = (points[:,2]*(zmax-zmin)+zmin) * np.sin(points[:,0]*np.pi)
points[:,0] *= 100
##group them into simlices
tri = Delaunay(points)
simplex_coords = np.array([tri.points[simplex] for simplex in tri.simplices])
##plotting the points
ax.scatter(points[:,0], points[:,1], points[:,2])
##visualizing simplices
line_coords = np.array(
[[c[i],c[j]] for c in simplex_coords for i in range(len(c)) for j in range(i+1,len(c))]
)
simplex_lines = Line3DCollection(line_coords, colors='k', linewidths=1, zorder=10)
ax.add_collection3d(simplex_lines)
##adjusting plot
ax.set_xlim([xmin,xmax])
ax.set_xlabel('x')
ax.set_ylim([2*ymin,2*ymax])
ax.set_ylabel('y')
ax.set_zlim([2*zmin,2*zmax])
ax.set_zlabel('z')
def compute_2D_outline():
"""
Compute the outline of the 2D projection of the 3D mesh and display it as
a Poly3DCollection or a Line3DCollection.
"""
global collection
global lines
global elev
global azim
##remove the previous projection (if it has been already created)
try:
collection.remove()
lines.remove()
except NameError as e:
pass
##storing current axes orientation
elev = ax.elev
azim = ax.azim
##convert angles
theta = -ax.elev*np.pi/180
phi = -ax.azim*np.pi/180
#the extend of each of the axes:
diff = lambda t: t[1]-t[0]
lx = diff(ax.get_xlim())
ly = diff(ax.get_ylim())
lz = diff(ax.get_zlim())
##to compute the projection, we 'unstretch' the axes and rotate them
##into the (elev=0, azmi=0) orientation
stretch = np.diag([1/lx,1/ly,1/lz])
rot_theta = np.array([
[np.cos(theta), 0, -np.sin(theta)],
[0, 1, 0],
[np.sin(theta), 0, np.cos(theta)],
])
rot_phi = np.array([
[np.cos(phi), -np.sin(phi), 0],
[np.sin(phi), np.cos(phi), 0],
[0,0,1],
])
rot_tot = np.dot(rot_theta,np.dot(rot_phi,stretch))
##after computing the outline, we will have to reverse this operation:
bstretch = np.diag([lx,ly,lz])
brot_theta = np.array([
[ np.cos(theta), 0, np.sin(theta)],
[0, 1, 0],
[-np.sin(theta), 0, np.cos(theta)],
])
brot_phi = np.array([
[ np.cos(phi), np.sin(phi), 0],
[-np.sin(phi), np.cos(phi), 0],
[0,0,1],
])
brot_tot = np.dot(np.dot(bstretch,brot_phi),brot_theta)
##To get the exact outline, we will have to compute the projection of each simplex
##separately and compute the convex hull of the projection. We then use shapely to
##compute the unity of all these convex hulls to get the projection (or shadow).
poly = None
for simplex in simplex_coords:
simplex2D = np.dot(rot_tot,simplex.T)[1:].T
hull = simplex2D[ConvexHull(simplex2D).vertices]
if poly is None:
poly = Polygon(hull)
else:
poly = poly.union(Polygon(hull))
##the 2D points of the final projection have to be made 3D and transformed back
##into the correct axes rotation
outer_points2D = np.array(poly.exterior.coords.xy)
outer_points3D = np.concatenate([[np.zeros(outer_points2D.shape[1])],outer_points2D])
outer_points3D_orig = np.dot(brot_tot, outer_points3D)
##adding the polygons
collection = Poly3DCollection(
[outer_points3D_orig.T], alpha=0.25, facecolor='b', zorder=-1
)
ax.add_collection3d(collection)
##adding the lines
lines = Line3DCollection(
[outer_points3D_orig.T], alpha=0.5, colors='r', linewidths=5, zorder=5
)
ax.add_collection3d(lines)
def on_move(event):
"""
For tracking rotations of the Axes3D object
"""
if event.inaxes == ax and (elev != ax.elev or azim != ax.azim):
compute_2D_outline()
fig.canvas.draw_idle()
##initial outline:
compute_2D_outline()
##the entire thing will only work correctly with an orthogonal view
ax.set_proj_type('ortho')
##saving ax.azim and ax.elev for on_move function
azim = ax.azim
elev = ax.elev
##adding on_move to the event queue
c1 = fig.canvas.mpl_connect('motion_notify_event', on_move)
plt.show()
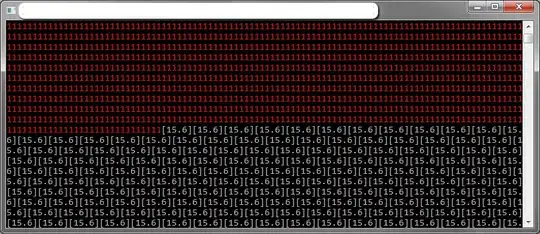
The final result (with some generated random data) looks something like this: