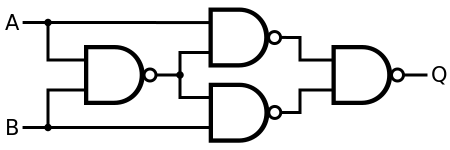
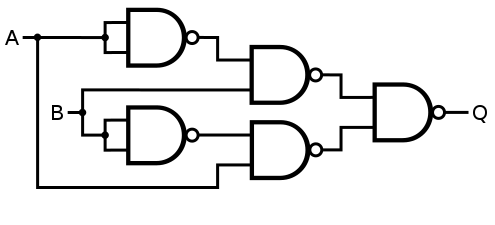
I had an interview question about implementing XOR in terms of ADD/SUB and branches:
Implement Xor operation between two numbers using the following commands only:
- Add
- Sub
- Branch if equal
- Branch if not equal
- And
You can use registers r3 and r4 as extra space. Assume that register r1 stores the first number and r2 stores the second number