I am using a calculating score based on the cosine similarity of the ideal values array and data collected array. (code below)
However, when I run the following code , the result is 99.4 which I think is weird because as 150 is very different with the ideal value 300.
import numpy as np
def cos_sim(speechrate, pitch): #speechrate and pitch are the data collected
v1 = np.array([300, 25]) #array of ideal values
v2 = np.array([speechrate, pitch]) #array of data
similarity = np.dot(v1, v2) / (np.linalg.norm(v1) * np.linalg.norm(v2))
print("{:.1f}".format(similarity*100))
cos_sim(150, 23)
Does anyone have any idea how to calculate the score based on the difference of the values? (not necessarily must use cosine similarity)
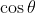 between the vectors
between the vectors 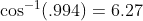 degrees, which is not much different from
degrees, which is not much different from