The algorithm is relatively simple. Instead of going one number at a time and accumulating the number of 1's its binary representation has, we will skip closer and closer to the target using a series of functions {a(m), b(m), c(m)...} to get closer to the target and leave at most a couple of numbers to add in manually in the end. Each function will be in the format 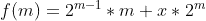 where x is the number of the function (for a(m) x=0, for b(m) x=1...).
where x is the number of the function (for a(m) x=0, for b(m) x=1...).
These functions are based on a trait of binary numbers: in all the numbers from 1 to
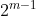 you can know the accumulated number of 1's in its binary representations of {1,2...n}.
you can know the accumulated number of 1's in its binary representations of {1,2...n}.
Let's look at the number 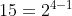 , which is in binary 1111. You can know the count of 1's in all the numbers from 1 (0001) to 15 (1111) - it's counting how many ways you can put 1 in 4 places (4) times 1, plus how many times you can put 2 in 4 places (6) times 2, plus how many times you can put 3 in 4 places (4) times 3 plus how many ways you can put 4 in 4 places (1) times 4. So the total is 32, which is also
, which is in binary 1111. You can know the count of 1's in all the numbers from 1 (0001) to 15 (1111) - it's counting how many ways you can put 1 in 4 places (4) times 1, plus how many times you can put 2 in 4 places (6) times 2, plus how many times you can put 3 in 4 places (4) times 3 plus how many ways you can put 4 in 4 places (1) times 4. So the total is 32, which is also 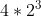 . you will notice that for any such number n=
. you will notice that for any such number n=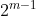 , the accumulated number of 1's is
, the accumulated number of 1's is 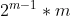 . Let's name this function a(m) as decided above (x=0 here, so no need for the added element in this one). For example:
. Let's name this function a(m) as decided above (x=0 here, so no need for the added element in this one). For example:
- 1 = a(1) =
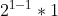 =
= 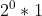 =
=  = 1.
= 1.
- 3 = a(2) =
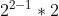 =
= 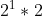 =
=  = 4.
= 4.
- 7 = a(3) =
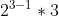 =
= 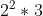 =
=  = 12.
= 12.
- 15 = a(4) =
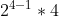 =
= 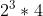 =
=  = 32.
= 32.
- 31 = a(5) =
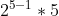 =
= 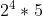 =
= 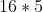 = 80.
= 80.
and so on. so for the number 15 which is 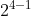 , we calculate a(4) and get 32 accumulated 1's. We will also notice that the number
, we calculate a(4) and get 32 accumulated 1's. We will also notice that the number 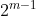 has exactly m 1's in it (all digits set to 1).
has exactly m 1's in it (all digits set to 1).
Knowing that, you take your number k find the nearest a(m) that's smaller than k, while a(m+1) will be greater than k. If a(m+1) is only m+1 more than k, take a(m+1) as the answer and finish the algorithm. Since a(m+1) has at least m+2 in it, it means you cannot accumulate all the k 1's you need without it.
If k is more than m+1 larger than a(m+1) but is larger than a(m), you will need a second step approximation by defining a second function - let's call it b(m). We'll define b(m)=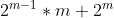 . This number will be equivalent to
. This number will be equivalent to 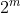 exactly (not
exactly (not 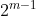 as it was for the a function) For example:
as it was for the a function) For example:
- 2 = b(1) =
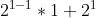 =
= 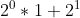 =
= 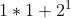 = 1+2 = 3.
= 1+2 = 3.
- 4 = b(2) =
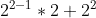 =
= 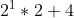 =
= 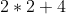 = 4+4 = 8.
= 4+4 = 8.
- 8 = b(3) =
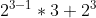 =
= 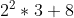 =
= 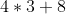 = 12+8 = 20.
= 12+8 = 20.
- 16 = b(4) =
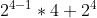 =
= 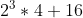 =
= 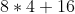 = 32+16 = 48.
= 32+16 = 48.
- 32 = b(5) =
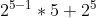 =
= 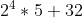 =
= 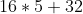 = 80+32 = 112.
= 80+32 = 112.
The reason we defined b is to describe the unique difference in accumulation of 1's between the first 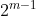 batch of numbers and the second following
batch of numbers and the second following 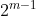 batch of numbers - the addition of another most-significant 1 to them each of the numbers in the second batch. This is why we now look at
batch of numbers - the addition of another most-significant 1 to them each of the numbers in the second batch. This is why we now look at 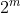 and not
and not 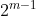 .
.
By adding the two functions, we can get our number n. If we still run short of the final k after two approximations, we can accumulate one by one the numbers until we reach k.
Let's assume k=50. We know that a(4) is the closest we can get, being the largest number that is still below 50. a(5) would get us to 80, as we saw above. So a(4) is the first half of the solution, which is 15.
The remaining 1's is 50-32=18. We need to see how many numbers we need to process past 15 to accumulate at least 18 more 1's. from calculating the b function, we see that b(2) gets us closer and b(3) is 2 over. Since we know that the number represented by b(3) has at least 4 1's in it, we know it's the number we need - any number below it will only have accumulated 16 1's and we need 18. So we go with b(3), which is 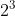 or 8. The result is 15+8=23, and that is the lowest number that has at least 50 accumulated 1's in all of the {1,2..23} binary representations.
or 8. The result is 15+8=23, and that is the lowest number that has at least 50 accumulated 1's in all of the {1,2..23} binary representations.
If we need to go another iteration, we can define 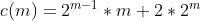 and it will get us even closer. For example, for k=120 we get a(5)+b(3)=100, and adding c(2) will add us 12 more to 112. We can add manually the missing 8 numbers or decide to add
and it will get us even closer. For example, for k=120 we get a(5)+b(3)=100, and adding c(2) will add us 12 more to 112. We can add manually the missing 8 numbers or decide to add 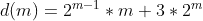 which will get us to 119 by adding a(5)+b(3)+c(2)+d(1). This means the next number must be the least n that has k or more 1's accumulated. a(5)=31, b(3)=8, c(2)=4 and d(1)=2 so n=46 - the next number up from the 119 1's collected by 45.
which will get us to 119 by adding a(5)+b(3)+c(2)+d(1). This means the next number must be the least n that has k or more 1's accumulated. a(5)=31, b(3)=8, c(2)=4 and d(1)=2 so n=46 - the next number up from the 119 1's collected by 45.
The complexity is O(log(k)) - we have log(k) steps to get a(m) and another at most log(k) accumulations to get the b(m) and our eventual n.
CODE
//This represents the function a(m), b(m)... etc.
public int getFuncResult(int funcNum, int arg) {
Double result = Math.pow(2,arg-1)*arg+funcNum*Math.pow(2,arg);
return result.intValue();
}
//This is the iterative algorithm described: add a(m)+b(m)... until k
public int countOnesToKIter(int k) {
int funcNum = 0;
int counter = 0;
int retVal = 0;
int exponent = 0;
while (k > 0) {
//for the current function, find the appropriate m
while (k > counter) {
exponent++;
counter = getFuncResult(funcNum, exponent);
}
//if the last number contains more 1's than the difference, use it.
if (counter-k < exponent) {
counter=getFuncResult(funcNum, exponent-2);
retVal+=Math.pow(2,exponent-2);
} else {
counter = getFuncResult(funcNum, exponent-1);
retVal+=Math.pow(2,exponent-1);
}
funcNum ++;
exponent=0;
k = k-counter;
counter = 0;
}
return retVal;
}
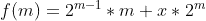 where x is the number of the function (for a(m) x=0, for b(m) x=1...).
where x is the number of the function (for a(m) x=0, for b(m) x=1...).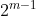 you can know the accumulated number of 1's in its binary representations of {1,2...n}.
you can know the accumulated number of 1's in its binary representations of {1,2...n}. 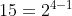 , which is in binary 1111. You can know the count of 1's in all the numbers from 1 (0001) to 15 (1111) - it's counting how many ways you can put 1 in 4 places (4) times 1, plus how many times you can put 2 in 4 places (6) times 2, plus how many times you can put 3 in 4 places (4) times 3 plus how many ways you can put 4 in 4 places (1) times 4. So the total is 32, which is also
, which is in binary 1111. You can know the count of 1's in all the numbers from 1 (0001) to 15 (1111) - it's counting how many ways you can put 1 in 4 places (4) times 1, plus how many times you can put 2 in 4 places (6) times 2, plus how many times you can put 3 in 4 places (4) times 3 plus how many ways you can put 4 in 4 places (1) times 4. So the total is 32, which is also 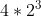 . you will notice that for any such number n=
. you will notice that for any such number n=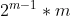 . Let's name this function a(m) as decided above (x=0 here, so no need for the added element in this one). For example:
. Let's name this function a(m) as decided above (x=0 here, so no need for the added element in this one). For example: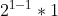 =
= 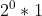 =
=  = 1.
= 1.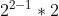 =
= 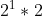 =
=  = 4.
= 4.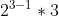 =
= 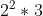 =
=  = 12.
= 12.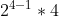 =
= 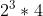 =
=  = 32.
= 32.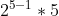 =
= 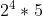 =
= 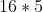 = 80.
= 80.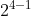 , we calculate a(4) and get 32 accumulated 1's. We will also notice that the number
, we calculate a(4) and get 32 accumulated 1's. We will also notice that the number 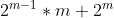 . This number will be equivalent to
. This number will be equivalent to 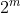 exactly (not
exactly (not 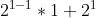 =
= 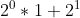 =
= 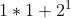 = 1+2 = 3.
= 1+2 = 3. 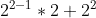 =
= 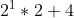 =
= 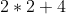 = 4+4 = 8.
= 4+4 = 8.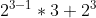 =
= 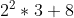 =
= 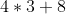 = 12+8 = 20.
= 12+8 = 20.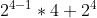 =
= 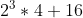 =
= 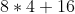 = 32+16 = 48.
= 32+16 = 48.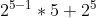 =
= 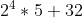 =
= 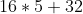 = 80+32 = 112.
= 80+32 = 112.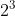 or 8. The result is 15+8=23, and that is the lowest number that has at least 50 accumulated 1's in all of the {1,2..23} binary representations.
or 8. The result is 15+8=23, and that is the lowest number that has at least 50 accumulated 1's in all of the {1,2..23} binary representations.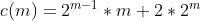 and it will get us even closer. For example, for k=120 we get a(5)+b(3)=100, and adding c(2) will add us 12 more to 112. We can add manually the missing 8 numbers or decide to add
and it will get us even closer. For example, for k=120 we get a(5)+b(3)=100, and adding c(2) will add us 12 more to 112. We can add manually the missing 8 numbers or decide to add 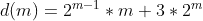 which will get us to 119 by adding a(5)+b(3)+c(2)+d(1). This means the next number must be the least n that has k or more 1's accumulated. a(5)=31, b(3)=8, c(2)=4 and d(1)=2 so n=46 - the next number up from the 119 1's collected by 45.
which will get us to 119 by adding a(5)+b(3)+c(2)+d(1). This means the next number must be the least n that has k or more 1's accumulated. a(5)=31, b(3)=8, c(2)=4 and d(1)=2 so n=46 - the next number up from the 119 1's collected by 45.