Suppose i have a dataset in [0,1]^d, that i want to symetrise in the sense that the repartition function of the "symmetrised" data, F, should hold the following assertion :
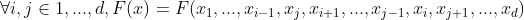
For exemple if d=2, the repartition function should be symetric around the first bissectrix :
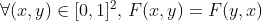
The transformation should be constructed from data. If you want some (trivariate) data to try working with, you can run the following R code (the package copula must be installed first) :
library(copula)
source(system.file("Rsource", "AC-Liouville.R", package="copula"))
U <- rLiouville(n=1000, alpha=c(1, 10,20), theta=0.6, Rdist="Gamma")
pairs(U)
Furthermore, i would like this transformation to be bijective, so that it could embbed a fit.
The main issue is the following : i have a fitting algorythme for symetric datasets and i want to extend it to non-symetric ones by the mean of this transformation, that i cant write properly...
Ideas ? Thank you :)