Binary Classification NN with Softmax Output Layer Predicting Incorrectly

Question

Quick Summary:

1. When I run my network with no activation function on its output layer and with the softmax_cross_entropy_with_logits_v2 loss function its predicted values are all negative and do not resemble my one hot output classes (which are just 0 or 1) which doesn't make sense to me. It seems to me that it would make sense to have the network itself output probabilities summing to 1 but I am unsure as to how to achieve this without using softmax as my output layer's activation function.

Already answered:

2. When I use softmax as my output class and cost = tf.reduce_mean(-tf.reduce_sum(y * tf.cast(tf.log(prediction), tf.float32), [1])) as my loss function (as referenced in the attached question), my network outputs all [nan, nan] predictions
3. When I tried softmax on the output layer and the softmax_cross_entropy_with_logits_v2 loss function together, all of my predictions were the same [0, 1] or [1, 0].

Longer Version:

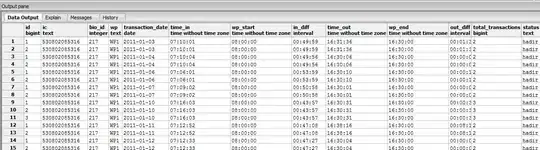
My data is of the form:

I have the following model which attempts to perform a binary classification using an output node of dimension 2.

def neural_network_model(data):

hidden_1_layer = {'weights': tf.Variable(tf.random_normal([n_features, n_nodes_hl1])),
                'biases': tf.Variable(tf.random_normal([n_nodes_hl1]))}
hidden_2_layer = {'weights': tf.Variable(tf.random_normal([n_nodes_hl1, n_nodes_hl2])),
                'biases': tf.Variable(tf.random_normal([n_nodes_hl2]))}
hidden_3_layer = {'weights': tf.Variable(tf.random_normal([n_nodes_hl2, n_nodes_hl3])),
                'biases': tf.Variable(tf.random_normal([n_nodes_hl3]))}
output_layer = {'weights':tf.Variable(tf.random_normal([n_nodes_hl3, n_classes])),
                'biases':tf.Variable(tf.random_normal([n_classes]))}

l1 = tf.add(tf.matmul(data, hidden_1_layer['weights']), hidden_1_layer['biases'])
l1 = tf.nn.relu(l1)

l2 = tf.add(tf.matmul(l1, hidden_2_layer['weights']), hidden_2_layer['biases'])
l2 = tf.nn.relu(l2)

l3 = tf.add(tf.matmul(l2, hidden_3_layer['weights']), hidden_3_layer['biases'])
l3 = tf.nn.relu(l3)
# output shape -- [batch_size, 2]
# example output = [[0.63, 0.37], 
#                   [0.43, 0.57]]
output = tf.add(tf.matmul(l3, output_layer['weights']), output_layer['biases'])
softmax_output = tf.nn.softmax(output)

return softmax_output, output

and I train it using the function below:

def train_neural_network(x):

softmax_prediction, regular_prediction = neural_network_model(x)

cost = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits_v2(logits=softmax_prediction, labels=y))
# cost = tf.reduce_mean(-tf.reduce_sum(y * tf.cast(tf.log(prediction), tf.float32), [1]))
optimizer = tf.train.AdamOptimizer(learning_rate=0.001).minimize(cost)

per_epoch_correct = tf.equal(tf.argmax(softmax_prediction, 1), tf.argmax(y, 1))
accuracy = tf.reduce_mean(tf.cast(per_epoch_correct, tf.float32))

hm_epochs = 5000
with tf.Session() as sess:
    sess.run(tf.global_variables_initializer())
    pred = []
    for epoch in range(hm_epochs):
        acc = 0
        epoch_loss = 0
        i = 0
        while i < len(X_train)-9:
            start_index = i
            end_index = i + batch_size

            batch_x = np.array(X_train[start_index:end_index])
            batch_y = np.array(y_train[start_index:end_index])

            _ , c, acc, pred = sess.run([optimizer, cost, accuracy, softmax_prediction], feed_dict={x: batch_x, y:batch_y})
            epoch_loss += c
            i += batch_size
        print(pred[0])
        print('Epoch {} completed out of {} loss: {:.9f} accuracy: {:.9f}'.format(epoch+1, hm_epochs, epoch_loss, acc))

    # get accuracy

    correct = tf.equal(tf.argmax(softmax_prediction, 1), tf.argmax(y, 1))
    final_accuracy = tf.reduce_mean(tf.cast(correct, tf.float32))
    print('Accuracy:', final_accuracy.eval({x:X_test, y:y_test})) 

So basically, my network "works" (I think?) when I run it with no activation function on its output layer and with the softmax_cross_entropy_with_logits_v2 loss function. However, when I look at its predicted values, they are all negative and do not resemble my one hot output classes (which are just 0 or 1) which doesn't make sense to me.

Furthermore, I was looking through this question regarding the proper way to use the softmax function and it seems to make sense for me to use softmax as my output layer's activation function. This is because I have 2 output classes and thus my network could output the probability of each class summing up to 1. However, when I use softmax as my output class and cost = tf.reduce_mean(-tf.reduce_sum(y * tf.cast(tf.log(prediction), tf.float32), [1])) as my loss function (as referenced in the attached question), my network outputs all [nan, nan] predictions. When I tried softmax on the output layer and the softmax_cross_entropy_with_logits_v2 loss function together, all of my predictions were the same [0, 1] or [1, 0]. I tried following the suggestions in this question but my network with softmax output still only outputs predictions of either all [0, 1] or [1, 0].

Overall, I am unsure as to how to procede and I believe that I must be misunderstanding how this network should be structured. Any help would be appreciated.

Answer 1

When you use cross_entropy_with_logits_v2 it is important that you pass the logit. It is called logit to previous value before applying the softmax. It should be like that:

cost = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits_v2(logits=regular_prediction, labels=y))

That function performs the softmax and then the cross_entropy. That is so because if they are applied separately in the backpropagation you could have numerical instability. But when applied at the same time, it is simplified in backpropagation and becomes 100% stable.

EDIT: cross_entropy_with_logits_v2 is a layer that does the following cross_entropy (softmax (x), y). The problem is that in the backward this combination of cross_entropy and then softmax is not numerically stable. That's why you get nans. When both are combined, a simplification is made in the following way: https://deepnotes.io/softmax-crossentropy

If you apply one and then the other, tensorflow would not have the ability to simplify.