Alternative to brute force estimation of parameter in an ecological time series model

Question

I am modeling a hydrologic process (water levels [stage] in lakes measured in mm) that can be described as:

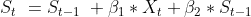
where 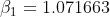is estimated from a different model and used as a constant in this model. 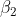is the unknown and the value is expected to be between (-0.001,0.001). The starting value of S doesn't matter so long as it is greater than 10m (10000mm). The model runs on a daily time step. I have observed stage from multiple different lakes and fit each lake independently.

Currently, I am brute-force identifying the parameter value by:

1. Creating a 100 value sequence of parameter values spanning (-0.001,0.001)
2. Predicting stage using the above equation and estimate RMSE between modeled and observed data (significantly fewer observations than modeled data points)
3. Identifying the B with the lowest RMSE and selecting B values on either side to create a new sequence of parameter values to search over
4. Step 2 and 3 are repeated until RMSE decreases by less than 0.01 or increases.

The code for the brute force approach I've been using is below along with the data associated with a single lake.

Is there an alternative approach to estimating the unknown parameter Beta2 given the model above and the fact that I only have observed data for a limited number of days?

Thanks!

library(tidyverse)
library(lubridate)
library(Metrics)

#The Data
dat <- read_csv("https://www.dropbox.com/s/skg8wfpu9274npb/driver_data.csv?dl=1")
observeddata <-    read_csv("https://www.dropbox.com/s/bhh27g5rupoqps3/observeddata.csv?dl=1") %>% select(Date,Value)

#Setup initial values and vectors
S = matrix(nrow = nrow(dat),ncol = 1) #create an empty matrix for predicted values
S[1,1] = 10*1000 #set initial value (mm)
rmse.diff <- 10^100 #random high value for difference between min RMSE between successive
                    #parameter searches
b.levels <- seq(from = -0.001,to = 0.001,length.out=100) #random starting parameter that should contain
                                                         #the final value being estimated 
n = 0 # counter

#Loop to bruteforce search for best parameter estimate
while(rmse.diff > 0.01 ) {
  rmse.vec = rep(NA,length(b.levels))
  for(t in 1:length(b.levels)){
    for(z in 2:nrow(S)){
      S[z,1] <- S[(z-1),1] + (1.071663*(dat$X[z])) + (b.levels[t]*(S[(z-1),1])) #-1.532236
    } #end of time series loop
    extrap_level <- data.frame(Date= dat$Date, level = S) # predicted lake levels

    #calculate an offset to center observed data on extrapolated data 
    dat.offset = observeddata %>% left_join(extrap_level) %>% 
      mutate(offset = level-Value) %>% drop_na()
    offset <- mean(dat.offset$offset)
    dat.compare <- observeddata %>% left_join(extrap_level) %>% 
      mutate(Value = Value + offset) %>% drop_na()
    #calculate RMSE between observed and extrapolated values
    rmse.vec[t] <- rmse(actual = dat.compare$Value,predicted = dat.compare$level)
    #plot the data to watch how parameter choice influences fit while looping
    #plots have a hard time keeping up
    if(t ==1 | t==50 | t==100) {
    plot(extrap_level$Date,extrap_level$level,type="l")
    lines(dat.compare$Date,dat.compare$Value,col="red")
    }
  }
  #find minimum RMSE value
  min.rmse <- which(rmse.vec==min(rmse.vec))
  if(n == 0) rmse.best <- rmse.vec[min.rmse] else rmse.best = c(rmse.best,rmse.vec[min.rmse])
  if (n >= 1) rmse.diff <- (rmse.best[n]-rmse.best[n+1])
  if(rmse.diff < 0) break()
  best.b <- b.levels[min.rmse]
  #take the parameter values on either side of the best prior RMSE and use those as search area
  b.levels <- seq(from = (b.levels[min.rmse-1]),to = (b.levels[min.rmse+1]),length.out=100)
  n = n + 1
}

rmse.best #vector of RMSE for each parameter search 
best.b #Last identified best parameter value