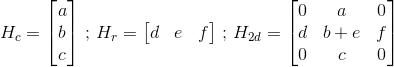Your project seems cool so I spend some times finding a solution. I came up the code below. The result of the code is:
OUTPUT[XNOR[NOR[AND[B, A], OR[D, C]], XOR[NOT[G], NAND[E, F]]]]
I made the assumptions that if an element is leftmost than another then it is a previous block. Also I assumed that in your set of lines the first one is correct... This allow me to simplify your 14 set of several lines into a set of 14 lines.
boxes = [['AND', (614, 98), (1146, 429)], ['NOT', (525, 1765), (1007, 1983)], ['NAND', (762, 1188), (1209, 1528)],
['NOR', (1323, 272), (1884, 682)], ['OR', (575, 599), (1225, 985)], ['XOR', (1393, 1368), (2177, 1842)],
['XNOR', (2136, 859), (2762, 1231)], ['A', (34, 50), (321, 224)], ['B', (12, 305), (344, 487)],
['C', (3, 581), (391, 779)], ['D', (0, 828), (400, 1060)], ['E', (0, 1143), (354, 1351)],
['F', (0, 1418), (313, 1615)], ['G', (0, 1753), (301, 1985)], ['OUTPUT', (2810, 940), (3069, 1184)]]
final_line_points = [[[(87, 1864), (625, 1869)]],
[[(623, 1815), (1354, 1855)], [(1343, 1660), (1770, 1655)], [(1348, 1656), (1348, 1869)]],
[[(102, 971), (531, 945)], [(518, 835), (892, 825)], [(521, 830), (526, 949)]],
[[(105, 1260), (494, 1254)], [(487, 1351), (891, 1340)], [(489, 1252), (491, 1356)]],
[[(107, 1533), (526, 1510)], [(516, 1432), (892, 1410)], [(521, 1433), (520, 1514)]],
[[(111, 432), (519, 396)], [(499, 313), (820, 299)], [(503, 310), (506, 402)]],
[[(123, 157), (496, 150)], [(493, 144), (498, 247)], [(495, 242), (815, 234)]],
[[(170, 692), (509, 687)], [(504, 771), (888, 764)], [(505, 685), (508, 775)]],
[[(936, 264), (1229, 261)], [(1227, 257), (1240, 485)], [(1234, 481), (1535, 458)]],
[[(985, 1361), (1343, 1347)], [(1341, 1344), (1348, 1578)], [(1345, 1575), (1773, 1571)]],
[[(991, 796), (1264, 778)], [(1240, 535), (1544, 520)], [(1247, 532), (1254, 783)]],
[[(1546, 582), (2156, 489)], [(2154, 488), (2148, 1021)]], [[(2153, 1087), (2164, 1581)]],
[[(2444, 1139), (3017, 1055)]]]
def dist(pt1, pt2):
return (pt1[0] - pt2[0]) ** 2 + (pt1[1] - pt2[1]) ** 2
def seg_dist(seg1, seg2):
distances = [dist(seg1[i], seg2[j]) for i in range(2) for j in range(2)]
return min(enumerate(distances), key=lambda x: x[1])
sorted_lines = []
for lines in final_line_points:
connected_part = lines[0]
non_connected = lines[1:]
while non_connected:
mat_dist = [seg_dist(connected_part, non_connected[i])[1] for i in range(len(non_connected))]
i, min_dist = min(enumerate(mat_dist), key=lambda x: x[1])
seg_to_connect = non_connected.pop(i)
idx, real_dist = seg_dist(connected_part, seg_to_connect)
if idx == 0:
print("error: this case is not handled")
exit()
elif idx == 1:
print("error: this case is not handled")
exit()
elif idx == 2:
connected_part[1] = seg_to_connect[1]
elif idx == 3:
connected_part[1] = seg_to_connect[0]
sorted_lines.append(connected_part)
class node():
def __init__(self, name, box) -> None:
super().__init__()
self.name = name
self.box = [(min(box[0][0], box[1][0]), min(box[0][1], box[1][1])),
(max(box[0][0], box[1][0]), max(box[0][1], box[1][1]))]
self.args = []
self.outputs = []
def __contains__(self, item):
return self.box[0][0] <= item[0] <= self.box[1][0] and self.box[0][1] <= item[1] <= self.box[1][1]
def __str__(self) -> str:
if self.args:
return f"{self.name}{self.args}"
else:
return f"{self.name}"
def __repr__(self) -> str:
return self.__str__()
def center(self):
return (self.box[0][0] + self.box[1][0]) / 2, (self.box[0][1] + self.box[1][1]) / 2
nodes = [node(box[0], box[1:]) for box in boxes]
for line in sorted_lines:
start_point = line[0]
end_point = line[1]
try:
gate1 = next(node for node in nodes if start_point in node)
gate2 = next(node for node in nodes if end_point in node)
if gate1.center() < gate2.center():
source_gate = gate1
dest_gate = gate2
else:
source_gate = gate2
dest_gate = gate1
source_gate.outputs.append(dest_gate)
dest_gate.args.append(source_gate)
except StopIteration:
print(f"{start_point} or {end_point} not in any of the boxes")
print(next(node for node in nodes if node.name == "OUTPUT"))
I can explain more another day if needed or you can start from here. Anyway have fun with your project.
EDIT:
My goal was to build a graph where the nodes are the boxes and the edges are the lines. The issue was that those lines are only defined as a set of closed lines. Also they were in disorder but the first. So the first step is to turn each set of lines into a straight line. That is what I called sorted_lines.
To build this list I used the following logic:
- For each set of lines split it into a connected part and a non connected part
- The initialization of the connected part is the first line of the set. As I said, here I assumed that the first line is correct. Try to improve this because this assumption may be wrong in other cases.
While there is non connected line do the following:
- Find the segment which has the closest end to the connected part
- Remove it from the non connected part
- Check which end of the segment is the closest from the connected part
- If it is the first point of the segment then the last point of the connected part becomes the second point of the segment else the first point becomes the last point.
In the checking the non handled cases are when the segment to connect is closed to the first point of the connected part instead of the last point. This is not handled because I assumed that the first line is correct. Once again, this can be improved.
Now that you have your lines sorted, for each one of them find the nodes containing each end. Select the lestmost as the source gate and the rightmost as the destination gate. Since edges are not oriented I had to assumed an orientation. Update the inputs of the destination gate and the outputs of the source gate.
Finally print the last gate of your graph.