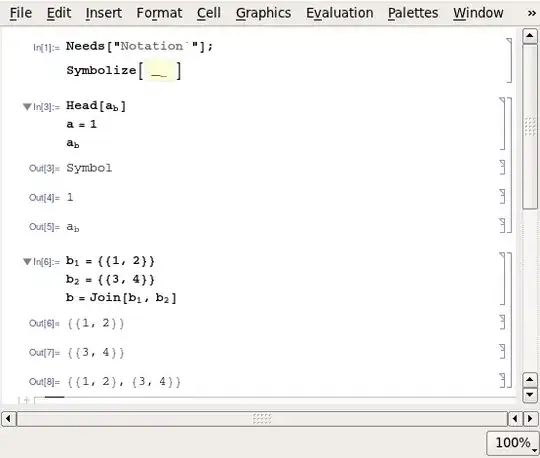
If you don't want to use the Notation package (see Daniel's and my answers) but want to copy the behaviour of Symbolize, then it gets a little tricky.
I had a go at doing this after I reading this SO answer but ran into troubles and gave up. I'll put the code here as community wiki so other people can try to finish it!
First you want to intercept an inputted subscript box structure and make it be interpreted as a "unique" symbol. The following code
MakeExpression[SubscriptBox[x_String, i_String], form_] :=
With[{name = StringJoin[{"$sUbsCript$", x, "$SPLIT$", i}]},
Hold[Symbol[name]]]
makes an inputted x_i become a symbol named "$sUbsCript$x$SPLIT$i". Not a guaranteed unique symbol name... but it would a fairly unusual one!
Notes:
1) that this code will not pick up subscripts written in FullForm.
2) this definition only fires off if both parts of the subscript are "simple" - no spaces, brackets, operators, etc...
Next, because this symbol name is so ugly, here's an optional something to make it nicer when it's asked for (this probably should be changed)
Protect[$inSymbolName];
Unprotect[SymbolName];
SymbolName[symb_Symbol] :=
Block[{$inSymbolName = True, result, s},
result = If[StringMatchQ[s = SymbolName[symb], "$sUbsCript$" ~~ __],
StringJoin@StringSplit[StringDrop[s, 11], "$SPLIT$"],
s]] /; ! TrueQ[$inSymbolName]
Protect[SymbolName];
Finally, we want this subscript symbol to print out nicely. Normally we'd do this using a MakeBoxes definition -- but we can't in this case because Symbol has the attribute Locked :(
Instead, we'll hack in a $PrePrint to find these crazily named symbols and write them back as subscripts:
$PrePrint = (# /. s_Symbol :>
Block[{$inSymbolName = True},
If[StringMatchQ[SymbolName[s], "$sUbsCript$" ~~ __],
Subscript@@StringSplit[StringDrop[SymbolName[s], 11], "$SPLIT$"], s]]
)&;
Finally the place where all of this falls down is if you try to assign something to a subscripted symbol. I haven't tried working around this yet!
Some tests - note that you'll have to convert the Subscripts to actual boxes for the code to work. Do this by converting to StandardForm: Ctrl-Shift-N.
symbs = {x, yy, Subscript[a, 3], Subscript[long, name]};
In[10]:= Head/@symbs
Out[10]= {Symbol, Symbol, Symbol, Symbol}
In[11]:= SymbolName/@symbs
Out[11]= {x, yy, a3, longname}
In[12]:= Block[{$inSymbolName=True},SymbolName/@symbs]
Out[12]= {x, yy, $sUbsCript$a$SPLIT$3, $sUbsCript$long$SPLIT$name}
In[13]:= f[x_Symbol] := Characters[SymbolName[x]]
In[14]:= {f["acb"], f[abc], f[Subscript[xx, 2]]}
Out[14]= {f["acb"], {"a", "b", "c"}, {"x", "x", "2"}}
It doesn't work with Set or SetDelayed if they generate OwnValues and it doesn't work with Information
In[15]:= Subscript[x, y] = 5
??Subscript[x, y]
During evaluation of In[4]:= Set::write: Tag Symbol in Symbol[$sUbsCript$x$SPLIT$y] is Protected. >>
Out[15]= 5
During evaluation of In[4]:= Information::nomatch: No symbol matching Symbol["$sUbsCript$x$SPLIT$y"] found. >>
It does work with definitions that produce DownValues
In[17]:= Subscript[x, z][z_]:=z^2
In[18]:= Subscript[x, z][2]
Out[18]= 4
In[19]:= ?Subscript[x, z]
Information::nomatch: No symbol matching Symbol["$sUbsCript$x$SPLIT$z"] found. >>