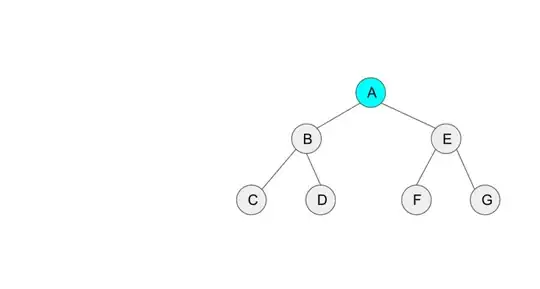
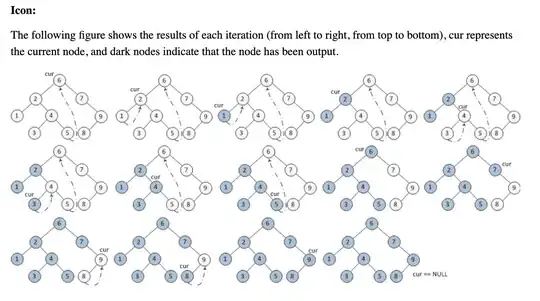
Can someone please help me understand the following Morris inorder tree traversal algorithm without using stacks or recursion ? I was trying to understand how it works, but its just escaping me.
1. Initialize current as root
2. While current is not NULL
If current does not have left child
a. Print current’s data
b. Go to the right, i.e., current = current->right
Else
a. In current's left subtree, make current the right child of the rightmost node
b. Go to this left child, i.e., current = current->left
I understand the tree is modified in a way that the current node, is made the right child of the max node in right subtree and use this property for inorder traversal. But beyond that, I'm lost.
EDIT:
Found this accompanying c++ code. I was having a hard time to understand how the tree is restored after it is modified. The magic lies in else clause, which is hit once the right leaf is modified. See code for details:
/* Function to traverse binary tree without recursion and
without stack */
void MorrisTraversal(struct tNode *root)
{
struct tNode *current,*pre;
if(root == NULL)
return;
current = root;
while(current != NULL)
{
if(current->left == NULL)
{
printf(" %d ", current->data);
current = current->right;
}
else
{
/* Find the inorder predecessor of current */
pre = current->left;
while(pre->right != NULL && pre->right != current)
pre = pre->right;
/* Make current as right child of its inorder predecessor */
if(pre->right == NULL)
{
pre->right = current;
current = current->left;
}
// MAGIC OF RESTORING the Tree happens here:
/* Revert the changes made in if part to restore the original
tree i.e., fix the right child of predecssor */
else
{
pre->right = NULL;
printf(" %d ",current->data);
current = current->right;
} /* End of if condition pre->right == NULL */
} /* End of if condition current->left == NULL*/
} /* End of while */
}