3

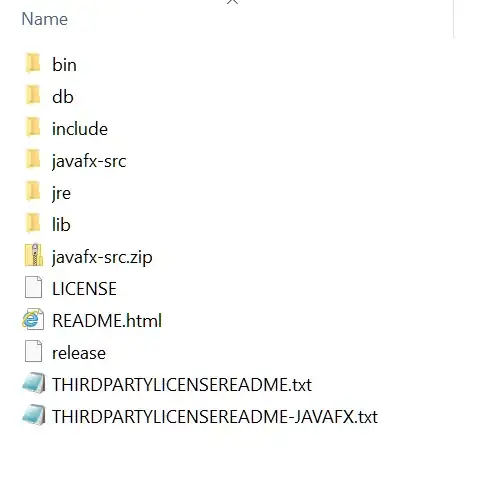
Intro.

Previously, I've asked a question on converting rgb triple to quaternion. After that question I've managed to get unit quaternions, but I am in doubt of their internal structure. There was no easy way to operate them, and to separate luma and chroma, since that were quaternions of unit length. According to my feeling about it, luminance should be encoded in the either real part, or a whole magnitude; And color "chroma" information should be encoded in the imaginary part.

Today I've decided to improve things up, taking another approach, different from the first one in the link above. I think it could success, since quaternion could store not only rotation(unit quaternion), but scale as well. First things first, so I'll start with explaining my next idea. I would use GLSL shader syntax in the following explanations.

Approach description and the question body.

For some pixel of an image, let's concieve a 3D vector vec3 u within the unit cube, where positive coordinates are lying in closed range [0.0, 1.0], and are representing full rgb colorspace. So now u's coordinates , u.x, u.y and u.z would represent red, green and blue values of that pixel, accordingly. Then lets take a pure white vector const vec3 v = vec3(1.0, 1.0, 1.0);. And let's define some quaternion q, so that our vector u is the "v, rotated and scaled with quaternion q". In simple words, q must answer the question "How to transform v, in order to get initially conceived color u?". And lets introduce function for that "rotate and scale" operation: vec3 q2c(in vec4 q, in vec3 v). I'll call it "quaternion-to-color" converter.

Writing q2c(q, v) is pretty simple, just as defined: q2c(q, v) == (q*vec4(v, 0.0))*q'. Here, the "*" operator denotes quaternion multiplication; Lets make it a function vec4 qmul(in vec4 q1, in vec4 q2). And "q'" denotes q's conjugate, lets make it vec4 qconj(in vec4 q). Omitting their simple implementation (that you may find in full source), we would come to classic code: 

vec4 q2c(in vec4 q, in vec3 v) {
    return qmul(qmul(q, vec4(v, 0.0)), qconj(q));
}

So now we have q2c(q,v) function, that converts quaternion q to color, by rotating and scaling some chosen 3D vector v.

The question is How to find that quaternion q?

From a programmer's perspective, the goal is To write reverse function vec4 c2q(in vec3 u, in vec3 v) - a corresponding "color to quaternion" converter.

Please note, that you should not touch q2c(), without a really good reason. E.g, a serious bug in its logic, leading to "impossibility to solve task", and you can proof that.

How could you check, if your answer is correct?

Indeed, the checking method would arise from the fact that you would get initial value, if you will manage to convert forth and back. So the checking condition is For any non-zero length v, u must always be equal to q2c(c2q(u, v), v). v must have non-zero length, because one cannot "scale zero" to get "something".

To easy things up, I've prepared testing program, using shadertoy.com service.

You would require a decent computer, with working internet connection and a web browser with webGL support (I'm using Chrome). Program should work on any GPU, even embedded into intel's processors. It even worked on my lower-end smartphone!

To test your answer, you should put your proposed formula, written in GLSL syntax, inside c2q() function. Then press apply button, and your changes will come into effect: enter image description here

Image at the left represents some unchanged source pixels. And right half will contain pixels, transformed forth and back by q2c(c2q()). Obviously, halves must be visually equal, you should not notice any vertical line. An some little mathematical(unnoticeable) error may arise, but only due to floating point's nature - its finite precision and possible rounding errors.

Feel free to edit and experiment, changes will be done only locally, on your computer, and you cannot wreck anything. If video is not playing on first open (shadertoy bug) - try to pause/unpause it. Enjoy!

Hall of c2q() Attempts

If everything is correct, the right side of image(processed one) should be equal to the left side(original). And here I would review different results, that were obtained by putting something instead of xxxxx, in the c2q() implementation:

vec4 c2q(vec3 u, vec3 v) {
    return xxxxx;
}

Lets proceed!

  • Initially I've thought that must just work: vec4(cross(u, v), dot(u, v)): enter image description here

  • One of SE answers: vec4( cross(u, v), sqrt( dot(u, u) * dot(v, v) ) + dot(u, v) ): enter image description here

  • And with his hint "Don't forget to normalize q": normalize(vec4( cross(u, v), sqrt( dot(u, u) * dot(v, v) ) + dot(u, v) )): enter image description here

  • @minorlogic's comment, seems to be a step closer: scale all q's components by sqrt( length(v)/length(u) ), vec4(cross(u, v), dot(u, v)) * sqrt( length(u)/length(v) ): enter image description here

  • With ratio swapped: vec4(cross(u, v), dot(u, v)) * sqrt( length(v)/length(u) ): enter image description here

Nicol Bolas
  • 449,505
  • 63
  • 781
  • 982
xakepp35
  • 2,878
  • 7
  • 26
  • 54
  • In compare to the link there are (+/-) differences in `qmul`. – Rabbid76 Apr 01 '19 at 19:18
  • @Rabbid76 That was not it, but a `q2c()`'s order of multiplications: `q * v * q'` vs `q' * v * q`. Swap it and you would get reverse rotation and *RGB* -> *CMY* color shift. I've managed to find it after an hour or so. Also, Rules were changed, question is now way more interesting and interactive ;-) – xakepp35 Apr 02 '19 at 21:14
  • https://stackoverflow.com/questions/1171849/finding-quaternion-representing-the-rotation-from-one-vector-to-another?noredirect=1&lq=1 – minorlogic Apr 04 '19 at 07:26
  • @minorlogic tested, present in "hall of shame" section, as well in the linked question section. Have you even tried to read the question?)) Or just searched SE, in a hope of duplicate? ;-p – xakepp35 Apr 04 '19 at 09:58
  • It is correct solution to described problem. So 1. Check your implementation for bugs ? Test result quat if it rotates "u" into "v" 2. If it works well , verify if problem is correct formulated – minorlogic Apr 04 '19 at 10:05
  • @minorlogic You may check yourself that it is incorrect. Implementation and testing framework is provided, source code is if order less than 1000 characters.. 4clicks: proceed to link, Comment line 25, Uncomment line 26, Press apply. – xakepp35 Apr 04 '19 at 10:08
  • if "u" don't rotates to "v", than check all of your math , including multiplication of vector by quaternion. – minorlogic Apr 04 '19 at 10:29
  • @minirlogic It rotates just fine, but scales inappropriate. Maybe trick is that it is **not only rotation** but should incorporate scale as well. And I am not so good at quaternion math, thus asked for some help.. Proposed Application is uncommon. Also I am trying to transform `v` to become `u` – xakepp35 Apr 04 '19 at 10:33
  • this formula for rotation only , without scaling. To apply scaling too, just scale quaternion by sqrt( ratio between "u" and "v" ) BWT. check again your multiplication. – minorlogic Apr 04 '19 at 10:44
  • @minorlogic Checked `qmul()` multiplication: it is correct. Checked multiple times, works in another projects very well! BTW, [here is the inverted version](https://www.euclideanspace.com/maths/algebra/realNormedAlgebra/quaternions/code/index.htm#mul). I've copied it, and it works same, just required swapping `q` with its `qconj(q)`, where multiplication order is expressed (inside `q2c()`) – xakepp35 Apr 04 '19 at 11:42
  • @minorlogic You said "*scale quaternion by sqrt*" - that is what I want to know! What quaternion, at which step, and how to scale? Whole? only w? preserve sign or not? Could you please write a formula?.. (in any form/language/pseudocode/whatever) – xakepp35 Apr 04 '19 at 11:43
  • quaternion of rotation "u" to "v", after c2q, scale all components , whole quaternion, sign of scale positive. scale as qscaled = q * sqrt( norm(v)/norm(u) ) here "norm" == length == magnitude – minorlogic Apr 04 '19 at 15:37
  • @minorlogic *probably*, that could be a step in a correct direction.. but not final answer. I've updated picture gallery - see last pics.. – xakepp35 Apr 04 '19 at 16:10
  • @xakepp35: Are you sure it's possible to use a quaternion to apply non-uniform scaling operations to a vector-to-vector transform? Indeed the answers to this Q&A suggest that [they can only represent uniform scaling](https://computergraphics.stackexchange.com/questions/138/when-should-quaternions-be-used-to-represent-rotation-and-scaling-in-3d). Equally importantly, why do you *want to*? – Nicol Bolas Apr 05 '19 at 02:10
  • @NicolBolas I thought of doing it in 3 steps. 1. Rotate `v` to be parallel with `u`. 2 scale `v` uniformly to be same length as `u`. 3 combine first two steps with `qmul` to get `q`. Is that possible?.. Color has 3 components. Quaternion has 4. So I **feel** that excessive component could be used to address uniform scale. But that s is not exactly.. Thus asked! – xakepp35 Apr 05 '19 at 04:07

1 Answers1

3

My attempt:

vec4 c2q(vec3 u, vec3 v) {
    float norm_q = sqrt(length(u) / length(v));
    vec4 u4 = vec4(normalize(u), 0.0);
    vec4 v4 = vec4(normalize(v), 0.0);
    return norm_q * (qmul(u4, v4 + u4) / length(v4 + u4));
}
Mauricio Cele Lopez Belon
  • 1,422
  • 1
  • 7
  • 9