I'm fitting a logarithmic curve to 20+ data sets using the equation
y = intercept + coefficient * ln(x)
Generated in R via
output$curvePlot <- renderPlot ({
x=medianX
y=medianY
Estimate = lad(formula = y~log(x),method = "EM")
logEstimate = lad(formula = y~log(x),method = "EM")
plot(x,predict(Estimate),type='l',col='white')
lines(x,predict(logEstimate),col='red')
points(x,y)
cf <- round(coef(logEstimate),1)
eq <- paste0("y = ", cf[1],
ifelse(sign(cf[2])==1, " + ", " - "), abs(cf[2]), " * ln(x) from 0 to ",xmax)
mtext(eq,3,line=-2,col = "red")
output$summary <- renderPrint(summary(logEstimate))
output$calcCurve <-
renderPrint(round(cf[2]*log(input$calcFeet)+cf[1]))
})
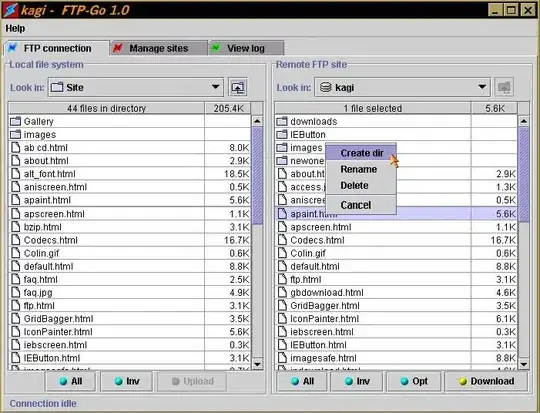
The curve consistently "crosses twice" on the data; fitting too low at low/high points on the X axis, fitting too high at the middle of the X axis.
I don't really understand where to go from here. Am I missing a factor or using the wrong curve?
The dataset is about 60,000 rows long, but I condensed it into medians. Medians were selected due to unavoidable outliers in the data, particularly a thick left tail, caused by our instrumentation.
x,y
2,6.42
4,5.57
6,4.46
8,3.55
10,2.72
12,2.24
14,1.84
16,1.56
18,1.33
20,1.11
22,0.92
24,0.79
26,0.65
28,0.58
30,0.34
32,0.43
34,0.48
36,0.38
38,0.37
40,0.35
42,0.32
44,0.21
46,0.25
48,0.24
50,0.25
52,0.23
Full methodology for context:
Samples of dependent variable, velocity (ft/min), were collected at various distances from fan nozzle with a NIST-calibrated hot wire anemometer. We controlled for instrumentation accuracy by subjecting the anemometer to a weekly test against a known environment, a pressure tube with a known aperture diameter, ensuring that calibration was maintained within +/- 1%, the anemometer’s published accuracy rating.
We controlled for fan alignment with the anemometer down the entire length of the track using a laser from the center of the fan, which aimed no more than one inch from the center of the anemometer at any distance.
While we did not explicitly control for environmental factors, such as outdoor air temperature, barometric pressure, we believe that these factors will have minimal influence on the test results. To ensure that data was collected evenly in a number of environmental conditions, we built a robot that drove the anemometer down the track to a different distance every five minutes. This meant that data would be collected at every independent variable position repeatedly, over the course of hours, rather than at one position over the course of hours. As a result, a 24 hour test would measure the air velocity at each distance over 200 times, allowing changes in temperature as the room warmed or cooled throughout the day to address any confounding environmental factors by introducing randomization.
The data was collected via Serial port on the hot wire anemometer, saving a timestamped CSV that included fields: Date, Time, Distance from Fan, Measured Temperature, and Measured Velocity. Analysis on the data was performed in R.
Testing: To gather an initial set of hypotheses, we took the median of air velocity at each distance. The median was selected, rather than the mean, as outliers are common in data sets measuring physical quantities. As air moves around the room, it can cause the airflow to temporarily curve away from the anemometer. This results in outliers on the low end that do not reflect the actual variable we were trying to measure. It’s also the case that, sometimes, the air velocity at a measured distance appears to “puff,” or surge and fall. This is perceptible by simply standing in front of the fan, and it happens on all fans at all distances, to some degree. We believe the most likely cause of this puffing is due to eddy currents and entrainment of the surrounding air, temporarily increasing airflow. The median result absolves us from worrying about how strong or weak a “puff” may feel, and it helps limit the effects on air speed of the air curving away from the anemometer, which does not affect actual air velocity, but only measured air velocity. With our initial dataset of medians, we used logarithmic regression to calculate a curve to match the data and generated our initial velocity profiles at set distances. To validate that the initial data was accurate, we ran 10 monte carlo folding simulations at 25% of the data set and ensured that the generated medians were within a reasonable value of each other.
Validation: Fans were run every three months and the monte carlo folding simulations were observed. If the error rate was <5% from our previous test, we validated the previous test.