How do I break a non-straight line into even segments?

Question

I have a non-straight line defined by a series of x, y coordinate points. I could draw a straight line on-screen directly between these points with no problem. Unfortunately, I have to draw the line in segments of equal length.

Here is an example of how I need to break up a non-straight line with 3 points into an array of several equidistant points. (ignore the final red dot, it is the result when a line does not divide evenly and is also the terminus)

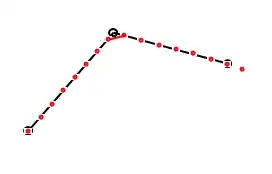
Please notice the red line at the "joint". Consider that I have a line A->B->C with the vectors AB and BC forming some angle. Basically, the line bends at point B.

Segmenting a line between point A and B is no problem up to a point. But when AB does not divide evenly by the segment length, I need to do something special. I need to take that remaining length and consider it as one side of a triangle. The constant segment length is another side of a triangle that connects with the BC segment (the red line above). I need to know the length from point B to this intersection. With this information, I can continue calculating line segments on BC.

Here is the triangle I am trying to solve (hereafter I will refer to the variables as they appear on this picture) So far I have broken down the problem to using the law of cosines. c² = a² + b² - 2ab * Cos(y)

The problem is that I already know c, it is the segment length. I need to solve for a (I can calculate y).

I've gotten as far as writing a polynomial equation, but now I am stuck: a² + b² - 2ab * Cos(y) - c² = 0

or Ax² + Bx + C (A = 1, B = -2b * Cos(y), C = b² - c², x = a)

Is this even the right approach? What do I do next? I need to implement this in Actionscript.

EDIT: Duh, I would have to use the quadratic formula. So I now get:

a = b * Cos(y) +/- SqrRoot(c² - b² * Sin(y)²)

Now how to put this into code...

Answer 1

Here's how I solved this. B and C are the same as you defined them, I'm calling Point A the end of the last full segment on the first line. (the last point before the bend) If you draw a circle with its center at A and a radius = your segment length, then where that circle intersects line BC is the endpoint (call it D) of a line from A that cuts your corner. To find that point, I found a neat helper function It's not very long and for simplicity, I'm just pasting it here.

/*---------------------------------------------------------------------------
Returns an Object with the following properties:
    enter           -Intersection Point entering the circle.
    exit            -Intersection Point exiting the circle.
    inside          -Boolean indicating if the points of the line are inside the circle.
    tangent     -Boolean indicating if line intersect at one point of the circle.
    intersects      -Boolean indicating if there is an intersection of the points and the circle.

If both "enter" and "exit" are null, or "intersects" == false, it indicates there is no intersection.

This is a customization of the intersectCircleLine Javascript function found here:

http://www.kevlindev.com/gui/index.htm

----------------------------------------------------------------------------*/
function lineIntersectCircle(A : Point, B : Point, C : Point, r : Number = 1):Object {
    var result : Object = new Object ();
    result.inside = false;
    result.tangent = false;
    result.intersects = false;
    result.enter=null;
    result.exit=null;
    var a : Number = (B.x - A.x) * (B.x - A.x) + (B.y - A.y) * (B.y - A.y);
    var b : Number = 2 * ((B.x - A.x) * (A.x - C.x) +(B.y - A.y) * (A.y - C.y));
    var cc : Number = C.x * C.x + C.y * C.y + A.x * A.x + A.y * A.y - 2 * (C.x * A.x + C.y * A.y) - r * r;
    var deter : Number = b * b - 4 * a * cc;
    if (deter <= 0 ) {
        result.inside = false;
    } else {
        var e : Number = Math.sqrt (deter);
        var u1 : Number = ( - b + e ) / (2 * a );
        var u2 : Number = ( - b - e ) / (2 * a );
        if ((u1 < 0 || u1 > 1) && (u2 < 0 || u2 > 1)) {
            if ((u1 < 0 && u2 < 0) || (u1 > 1 && u2 > 1)) {
                result.inside = false;
            } else {
                result.inside = true;
            }
        } else {
            if (0 <= u2 && u2 <= 1) {
                result.enter=Point.interpolate (A, B, 1 - u2);
            }
            if (0 <= u1 && u1 <= 1) {
                result.exit=Point.interpolate (A, B, 1 - u1);
            }
            result.intersects = true;
            if (result.exit != null && result.enter != null && result.exit.equals (result.enter)) {
                result.tangent = true;
            }
        }
    }
    return result;
}

It's a function that returns an object with several properties, so to implement in your code it's very simple. You need to pass it three points and a radius. The first two points are just B and C as you defined them above, and Point A as I explained at the beginning. The radius, again, is your segment length.

//create an object
var myObject:Object = lineIntersectCircle(pointB, pointC, pointA, segmentLength);

That's it! The coordinates of point D (see above) are: (myObject.exit.x, myObject.exit.y)