The objective of displaying an ellipse around the data points is to show the confidence interval, or in other words, "how much of the data is within a certain standard deviation way from the mean"
In the above code, he has chosen to display an ellipse that covers 95% of the data points. For a normal distribution, ~67% of the data is 1 s.d. away from the mean, ~95% within 2 s.d. and ~99% within 3 s.d. (the numbers are off the top of my head, but you can easily verify this by calculating the area under the curve). Hence, the value STD=2; You'll find that conf is approx 0.95.
The distance of the data points from the centroid of the data goes something like (xi^2+yi^2)^0.5, ignoring coefficients. Sums of squares of random variables follow a chi-square distribution and hence to get the corresponding 95 percentile, he uses the inverse chi-square function, with d.o.f. 2, as there are two variables.
Lastly, the rationale behind multiplying the scaling constant follows from the fact that for a square matrix A with eigenvalues a1,...,an, the eigenvalues of a matrix kA, where k is a scalar is simply ka1,...,kan. The eigenvalues give the corresponding lengths of the major/minor axis of the ellipse, and so scaling the ellipse or the eigenvalues to the 95%tile is equivalent to multiplying the covariance matrix with the scaling factor.
EDIT
Cheng, although you might already know this, I suggest that you also read this answer to a question on randomness. Consider a Gaussian random variable with zero mean, unit variance. The PDF of a collection of such random variables looks like this
Now, if I were to take two such collections of random variables, square them separately and add them to form a single collection of a new random variable, its distribution looks like this
This is the chi-square distribution with 2 degrees of freedom (since we added two collections).
The equation of the ellipse in the above code can be written as x^2/a^2 +y^2/b^2=k, where x,y are the two random variables, a and b are the major/minor axes, and k is some scaling constant that we need to figure out. As you can see, the above can be interpreted as squaring and adding two collections of Gaussian random variables, and we just saw above what its distribution looks like. So, we can say that k is a random variable that is chi-square distributed with 2 degrees of freedom.
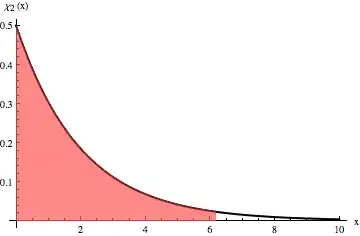
Now all that needs to be done is to find a value for k such that 95%ile of the data is within it. Just like the 1s.d, 2s.d, 3s.d. percentiles that we're familiar with Gaussians, the 95%tile for chi-square with 2 degrees of freedom is around 6.18. This is what Amro obtains from the chi2inv function. He could have just as well written scale=chi2inv(0.95,2) and it would have been the same. It's just that talking in terms of n s.d. away from the mean is intuitive.
Just to illustrate, here's a PDF of the chi-square distribution above, with 95% of the area < some x shaded in red. This x is ~6.18.
Hope this helped.



