This might be a solution for your problem.
This is the data I have used (identical to yours):
library(tidyverse)
library(lpSolve)
N <- 1000
set.seed(123)
df <- tibble(avg_points = sample(5:45,N, replace = T),
cost = sample(3:45,N, replace = T),
position = sample(c("P","C","1B","2B","3B","SS","OF"),N, replace = T),
team = sample(LETTERS,N, replace = T)) %>%
mutate(id = row_number())
You want to find x1...xn that maximise the objective function below:
x1 * average_points1 + x2 * average_points1 + ... + xn * average_pointsn
With the way lpSolve works, you will need to express every LHS as the sum over
x1...xn times the vector you provide.
Since you cannot express the number of teams with your current variables, you can introduce new ones (I will call them y1..yn_teams and z1..zn_teams):
# number of teams:
n_teams = length(unique(df$team))
Your new objective function (ys and zs will not influence your overall objective funtion, since the constant is set to 0):
obj <- c(df$avg_points, rep(0, 2 * n_teams))
)
The first 3 constraints are the same, but with the added constants for y and z:
c1 <- t(model.matrix(~ position + 0,df))
c1 <- cbind(c1,
matrix(0, ncol = 2 * n_teams, nrow = nrow(c1)))
c2 = df$cost
c2 <- c(c2, rep(0, 2 * n_teams))
c3 = t(model.matrix(~ team + 0, df))
c3 <- cbind(c3, matrix(0, ncol = 2 * n_teams, nrow = nrow(c3)))
Since you want to have at least 3 teams, you will first use y to count the number of players per team:
This constraint counts the number of players per team. You sum up all players of a team that you have picked and substract the corresponding y variable per team. This should be equal to 0. (diag() creates the identity matrix, we do not worry about z at this point):
# should be x1...xn - y1...n = 0
c4_1 <- cbind(t(model.matrix(~team + 0, df)), # x
-diag(n_teams), # y
matrix(0, ncol = n_teams, nrow = n_teams) # z
) # == 0
Since each y is now the number of players in a team, you can now make sure that z is binary with this constraint:
c4_2 <- cbind(t(model.matrix(~ team + 0, df)), # x1+...+xn ==
-diag(n_teams), # - (y1+...+yn )
diag(n_teams) # z binary
) # <= 1
This is the constraint that ensures that at least 3 teams are picked:
c4_3 <- c(rep(0, nrow(df) + n_teams), # x and y
rep(1, n_teams) # z >= 3
)
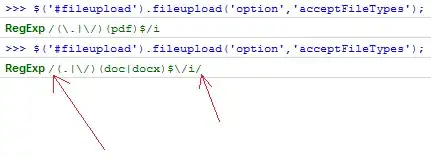
You need to make sure that
You can use the big-M method for that to create a constraint, which is:
Or, in a more lpSolve friendly version:
In this case you can use 6 as a value for M, because it is the largest value any y can take:
c4_4 <- cbind(matrix(0, nrow = n_teams, ncol = nrow(df)),
diag(n_teams),
-diag(n_teams) * 6)
This constraint is added to make sure all x are binary:
#all x binary
c5 <- cbind(diag(nrow(df)), # x
matrix(0, ncol = 2 * n_teams, nrow = nrow(df)) # y + z
)
Create the new constraint matrix
con <- rbind(c1,
c2,
c3,
c4_1,
c4_2,
c4_3,
c4_4,
c5)
#set the constraint values
rhs <- c(1,1,1,1,3,2,1, # 1. #exactly 3 outfielders 2 pitchers and 1 of everything else
200, # 2. at a cost less than 200
rep(6, n_teams), # 3. max number from any team is 6
rep(0, n_teams), # c4_1
rep(1, n_teams), # c4_2
3, # c4_3,
rep(0, n_teams), #c4_4
rep(1, nrow(df))# c5 binary
)
#set the direction of the constraints
dir <- c(rep("==", 7), # c1
"<=", # c2
rep("<=", n_teams), # c3
rep('==', n_teams), # c4_1
rep('<=', n_teams), # c4_2
'>=', # c4_3
rep('<=', n_teams), # c4_4
rep('<=', nrow(df)) # c5
)
The problem is almost the same, but I am using all.int instead of all.bin to make sure the counts work for the players in the team:
result <- lp("max",obj,con,dir,rhs,all.int = TRUE)
Success: the objective function is 450
roster <- df[result$solution[1:nrow(df)] == 1, ]
roster
# A tibble: 10 x 5
avg_points cost position team id
<int> <int> <chr> <chr> <int>
1 45 19 C I 24
2 45 5 P X 126
3 45 25 OF N 139
4 45 22 3B J 193
5 45 24 2B B 327
6 45 25 OF P 340
7 45 23 P Q 356
8 45 13 OF N 400
9 45 13 SS L 401
10 45 45 1B G 614
If you change your data to
N <- 1000
set.seed(123)
df <- tibble(avg_points = sample(5:45,N, replace = T),
cost = sample(3:45,N, replace = T),
position = sample(c("P","C","1B","2B","3B","SS","OF"),N, replace = T),
team = sample(c("A", "B"),N, replace = T)) %>%
mutate(id = row_number())
It will now be infeasable, because the number of teams in the data is less then 3.
You can check that it now works:
sort(unique(df$team))[result$solution[1027:1052]==1]
[1] "B" "E" "I" "J" "N" "P" "Q" "X"
sort(unique(roster$team))
[1] "B" "E" "I" "J" "N" "P" "Q" "X"


