Possible string permutations of mixture of multiset and set

Question

I am trying to get all possible combinations of a char*. This string consits of four values: two numbers and two different letters. For example:

char *text = "01ab";

There should be

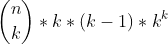
$\binom{n}{k}*k*(k-1)*k^{k}$

so

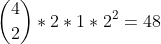
$\binom{4}{2}*2*1*2^{2} = 48$

different combinations for my example string, which seems to be true (done by hand):

Combinations for values: 0, 1, a, b:

0 0 a b     1 1 a b     a 0 0 b     b 0 0 a
0 0 b a     1 1 b a     a 0 1 b     b 0 1 a
0 1 a b     1 0 a b     a 0 b 0     b 0 a 0
0 1 b a     1 0 b a     a 0 b 1     b 0 a 1
0 a 0 b     1 a 1 b     a 1 b 0     b 1 0 a
0 a 1 b     1 a 0 b     a 1 b 1     b 1 1 a
0 a b 0     1 a b 1     a 1 0 b     b 1 a 0
0 a b 1     1 a b 0     a 1 1 b     b 1 a 1
0 b 0 a     1 b 1 a     a b 0 0     b a 0 0
0 b 1 a     1 b 0 a     a b 0 1     b a 0 1
0 b a 0     1 b a 1     a b 1 0     b a 1 0
0 b a 1     1 b a 0     a b 0 0     b a 1 1

My approach would be the same as the one I did by hand: get all combinations with the first index of text at the start, then all combinations of the second index of text and so on. So something like this:

void printPasswordCombinations()
{
    char *all_values = "01ab";
    int len = strlen(all_values);

    char *tmp_pwd = malloc(sizeof(len) * sizeof(char));

    for(int i=0 ; i<len ; i++)
    {
        tmp_pwd[0] = all_values[i];

        /* len-1, since the first index is already set. */
        for(int j=0 ; j<len-1 ; j++)
        {

        }
    }

    printf("%s\n", tmp_pwd);
    free(tmp_pwd);
}

Now I am a bit confused about how to continue after the first index of the combination. There are several examples for all combinations, but my problem seems to be a bit different, since my the numbers in the combination could be the same and only the letters have to be different.

How could I achieve to print all combinations to my console? I implemented a function which calculates the amount of possible combinations, so just assume this is already done.

It would be nice if the algorithm would work for any amounts of numbers and letters, so for example all combinations of a text of lenght 6 with four different numbers and two different letters could also be calculated.

The language doesn't matter, any advice is appreciated.

The first problem of your question is in the title. These are not combinations of "char pointer", they're *permutations of string". When you know the search keywords you'll find the solutions with google. — Antti Haapala -- Слава Україні, Apr 19 '19 at 19:37
@AnttiHaapala, this question is not a duplicate of the linked question. Here the op is dealing with permutations of multisets. — Joseph Wood, Apr 19 '19 at 19:42
@JosephWood ahem, right, the question is unclear. Trying to find a duplicate. — Antti Haapala -- Слава Україні, Apr 19 '19 at 19:45
Shall i change the title to permutations of multists? I was not sure how this kind of problem is called. — Moritz Schmidt, Apr 19 '19 at 20:38
@MoritzSchmidt - permutations of mixture of multiset and set. — niry, Apr 19 '19 at 21:27
@AnttiHaapala, the question title is now clear, and not a dup of the linked question. Will you reopen the question? — niry, Apr 20 '19 at 06:54

TaQuangTu · Answer 1 · 2019-04-19T17:05:10.363

Your problem can be solved by backtracking strategy. It will create all possible combinations.

I know you want to remove duplicate combinations in case the two number are the same, to get rid of them, you can use a hash table to store generated combination, and then, each time you generate a new combination, bring it to the hash table to check if it was generated or not(if not, enter it to the hash table and print it out, ignore printing in vice versa). There for my pseudocode as follow (you can have a better way):

val characters = [/*4 characters*/]
val picked = [false,false,false,false]
val hashtable = empty

function genetate(string aCombin):
    if aCombin.size == 4:
         if(hashtable.contains(aCombin)):
               //do nothing
         else:
               print(aCombin)
               hashtable.add(aCombin)
    for i in characters.size:
         if(picked[i]==false):
             picked[i]=true
             aCombin.add(characters[i])
             generate(aCombin)
             picked[i]=false //backtrack
             aCombine.popBack() //remove the last character

score 1 · Answer 2 · answered Apr 19 '19 at 16:57

A recursive approach would be the easy way here.
Let's consider that you want to generate all strings with m letters, all of them distinct, taken from a letters[m] array, and n numbers, that can be repeated, taken from a numbers[N] array (n can be smaller, of same size of bigger than N, it does not really matter).
You can solve it this way then (pseudo code, C style):

void print_them_all(char *numbers, int nb_numbers_in_result, int n              \
                    char *letters, bool *is_letter_used, int nb_letters_in_result, int m,
                    char *current_string){
    if ((nb_numbers_in_result == n) && (nb_letters_in_result == m)){
        // terminal case -> time to print the  current string
        printf("%s\n", current_string);
    } else {  
        // string not completely built yet
        // get the index where the next char will be added
        current_index = nb_letters_in_result + nb_numbers_in_result;
        if (nb_numbers_in_result < n){  // still possible to add a number
            for (int i = 0; i < N; i++){
                current_string[current_index] = numbers[i];
                print_them_all(numbers, nb_numbers_in_result+1, n,               \
                               letters, is_letter_used, nb_letters_in_result, m, \
                               current_string);
            }
        }
        if (nb_letters_in_result < m){ // still possible to add a letter
             for (int i = 0; i < m; i++) {
                 if (is_letter_used[i] == false){ // check the letter has not been added yet
                     // keep track that the letter has been added by 'marking' it
                     is_letter_used[i] = true;  
                     // add it
                     current_string[i] = letters[i];
                     // recursive call
                     print_them_all(numbers, nb_numbers_in_result, n,                   \
                                    letters, is_letter_used, nb_letters_in_result+1, m,  \ 
                                    current_string);
                     // now 'unmark' the letter
                     is_letter_used[i] = false;
                 }
             }
        }
    }
}

To solve this kind of problem, the recursive approach is necessary. It works as follows:
if I have a string with k numbers in it already, k<n, then I can add any number to it, and I can continue (now my string will have k+1 numbers in it).
If I have a string with k letters in it already, k<m, then I can add any letter that was not added already (the array of booleans helps to make sure it is the case), and I can continue. If my string is ready for print, print it.

The first call should be done with the boolean array initialized to false everywhere, and 0 for the values of nb_letters_in_result and nb_numbers_in_result, since you have not added any number or letter in your result string yet.
As for your result string, since you code in C, don't forget to allocate memory for it:

char *current_string = malloc((m+n+1) * sizeof(char));

and to null-terminate it:

current_string[m+n] = '\0';

niry · Accepted Answer · 2019-04-19T20:20:32.577

I used Javascript because it can run in browser and language doesn't matter. The below method uses recursion. Try it with '0123ab'.

'use strict';

const input = '01ab';

const reLetters = /[^0-9]/g;
const reDigits = /[0-9]/g;
const nLetters = input.replace(reDigits, '').length;
const nDigits = input.replace(reLetters, '').length;

const findComb = cur => {
    if (cur.length === input.length)
        return console.log(cur);
    for (let l of input) {
        if (l.match(reDigits)) {
            if (cur.replace(reLetters, '').length === nDigits) continue;
        } else {
            if (cur.match(l) || cur.replace(reDigits, '').length === nLetters) continue;
        }
        findComb(cur + l);
    }
}

findComb('');

Here is a version without "removing letters to count digits". it is about 20% more efficient. I used nodejs and '01234abc' as input to measure.

'use strict';

const input = '01ab';

const reLetters = /[^0-9]/g;
const reDigits = /[0-9]/g;
const maxLetters = input.replace(reDigits, '').length;
const maxDigits = input.replace(reLetters, '').length;

const findComb = (cur = '', nDigits = 0, nLetters = 0) => {
    if (cur.length === input.length)
        return console.log(cur);
    for (let l of input) {
        if (l.match(reDigits)) {
            if (nDigits < maxDigits)
                findComb(cur + l, nDigits + 1, nLetters);
        } else {
            if (cur.match(l)) continue;
            if (nLetters < maxLetters)
                findComb(cur + l, nDigits, nLetters + 1);
        }
    }
}

findComb();

Here it is without recursion. This is slowest of all, but can be improved.

'use strict';

const input = '01ab';

const reLetters = /[^0-9]/g;
const reDigits = /[0-9]/g;
const nLetters = input.replace(reDigits, '').length;
const nDigits = input.replace(reLetters, '').length;

let cur = '', l = undefined;
do {
    l = input[input.indexOf(l) + 1];
    if (l !== undefined) {
        if (l.match(reDigits)) {
            if (cur.replace(reLetters, '').length === nDigits) continue;
        } else {
            if (cur.match(l) || 
                cur.replace(reDigits, '').length === nLetters) continue;
        }
        if (cur.length + 1 === input.length) {
            console.log(cur + l);
        } else {
            cur = cur + l;
            l = undefined;
        }
    } else {
        l = cur[cur.length - 1];
        cur = cur.slice(0, -1);
    }
} while (cur != '' || l != undefined);

I chose your answer to be correct, since I could test it easily and the shortness of the code. Thanks for your effort. — Moritz Schmidt, Apr 19 '19 at 18:02
By the way, do you have any idea how this kind of combination is called? — Moritz Schmidt, Apr 19 '19 at 19:05
@MoritzSchmidt Sorry, I don't know. On a different topic, I'll add another piece of code which is more optimal. The current 'remove letters to count digits' is dumb idea and bugs me. — niry, Apr 19 '19 at 19:11
It would also be interesting how this could be solved without recursion, since my stack will explode if I want to do this with larger alphabets — Moritz Schmidt, Apr 19 '19 at 19:15
@MoritzSchmidt you'll need really long string to explode the stack, plus every recursion can be written as a loop, just need bit more code... I'll post one for fun — niry, Apr 19 '19 at 19:23

Moritz Schmidt · Answer 4 · 2019-04-21T02:28:34.797

I also found an interesting solution for my question. Assume my example string 01ab.

First we want to create all combinations of the numbers 01 and the permutation of ab. There are plenty examples of how to solves this.

So now we have all combinations of 01 and ab. I will call them producer combinations:

Now we want to combine all numbers with all letters but with the rule

The order of the numbers or letters must not be reserved for each combination

So if we combine 10 with ab we get:

10ab
1a0b
a10b

now we move b to the left side until it is about to swap its place with a, which is forbidden because of my rule. We do this for every combination:

10ab produces:

10ab

since b is already next to a.

1a0b produces:

1ab0

so we got one more combination.

a10b produces:

a1b0
ab10

so we got 2 more combinations.

Now we have all possible combinations for 01 and ab:

10ab
1a0b
a10b
1ab0
a1b0
ab10

Since our producer combinations contain 8 elements we have to do this step 8 times with all elements. The resulting combinations will always contain 6 elements like in my example which leads us to 48 elements in total as I calculated in my question.

Is there a name for this algorithm? – Moritz Schmidt Apr 20 '19 at 11:33 — Moritz Schmidt, Apr 20 '19 at 11:33

Possible string permutations of mixture of multiset and set

4 Answers4