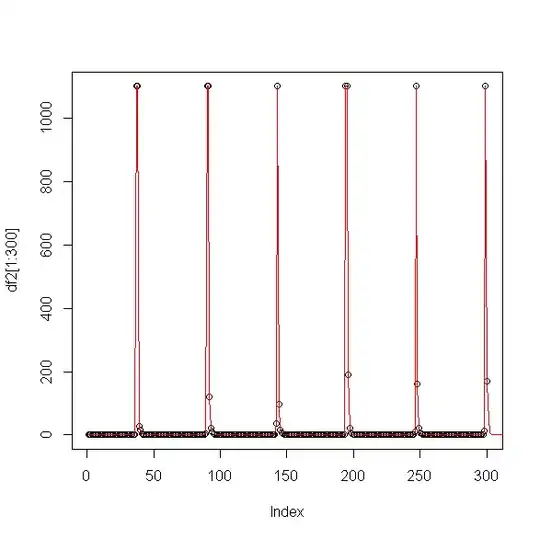
I'm currently working on data which contains 4 variables. I'm using only one at the moment. This variable contains low and high values.
I would like to extract all the values which represent a peak. Then I could examine the variability of these (cloud of dots).
Here is a graphic of my initial data (it represents the 300 first values) :
Here is an other grahic which overlay cycle:
Here are the values I would like to extract (I didn't surround all the values) :

The first 300 values :
c(0.096, 0.088, 0.082, 0.078, 0.06, 0.057, 0.048, 0.047, 0.044,
0.044, 0.039, 0.038, 0.037, 0.037, 0.035, 0.035, 0.034, 0.034,
0.033, 0.033, 0.032, 0.032, 0.031, 0.031, 0.031, 0.031, 0.03,
0.03, 0.03, 0.03, 0.03, 0.029, 0.029, 0.029, 0.029, 0.2, 1100,
1100, 27, 15, 3.2, 2.2, 1, 0.65, 0.37, 0.3, 0.19, 0.16, 0.12,
0.12, 0.099, 0.096, 0.085, 0.082, 0.064, 0.06, 0.051, 0.05, 0.046,
0.045, 0.041, 0.041, 0.039, 0.038, 0.037, 0.036, 0.035, 0.035,
0.034, 0.033, 0.032, 0.032, 0.032, 0.031, 0.031, 0.031, 0.03,
0.03, 0.03, 0.03, 0.029, 0.029, 0.029, 0.029, 0.029, 0.028, 0.028,
0.028, 4.4, 1100, 1100, 120, 21, 9.4, 3.1, 1.6, 0.85, 0.51, 0.33,
0.23, 0.18, 0.18, 0.13, 0.11, 0.1, 0.092, 0.085, 0.077, 0.065,
0.058, 0.053, 0.05, 0.047, 0.045, 0.043, 0.042, 0.039, 0.038,
0.037, 0.036, 0.035, 0.035, 0.034, 0.033, 0.033, 0.032, 0.031,
0.031, 0.031, 0.03, 0.03, 0.03, 0.029, 0.029, 0.029, 0.029, 0.028,
0.028, 0.028, 0.028, 0.028, 37, 1100, 98, 17, 6.2, 2.7, 1.3,
1, 0.47, 0.31, 0.23, 0.16, 0.14, 0.11, 0.1, 0.093, 0.087, 0.079,
0.066, 0.057, 0.053, 0.049, 0.046, 0.044, 0.041, 0.04, 0.037,
0.036, 0.035, 0.035, 0.033, 0.033, 0.032, 0.032, 0.031, 0.031,
0.03, 0.03, 0.029, 0.029, 0.029, 0.029, 0.028, 0.028, 0.028,
0.027, 0.027, 0.027, 0.026, 0.026, 0.026, 2.6, 1100, 1100, 190,
22, 7.8, 3.2, 2.2, 0.91, 0.51, 0.37, 0.23, 0.18, 0.14, 0.12,
0.11, 0.098, 0.09, 0.085, 0.071, 0.061, 0.055, 0.051, 0.049,
0.045, 0.043, 0.04, 0.039, 0.037, 0.036, 0.035, 0.034, 0.033,
0.032, 0.032, 0.031, 0.031, 0.03, 0.03, 0.03, 0.029, 0.029, 0.028,
0.028, 0.028, 0.027, 0.027, 0.027, 0.026, 0.026, 0.026, 0.026,
0.026, 8.8, 1100, 160, 21, 7.5, 3.4, 1.6, 0.89, 0.52, 0.33, 0.23,
0.17, 0.14, 0.13, 0.1, 0.094, 0.087, 0.078, 0.065, 0.056, 0.051,
0.049, 0.045, 0.043, 0.039, 0.039, 0.036, 0.035, 0.034, 0.033,
0.032, 0.032, 0.031, 0.03, 0.03, 0.03, 0.029, 0.029, 0.028, 0.028,
0.027, 0.027, 0.026, 0.026, 0.026, 0.026, 0.025, 0.025, 0.025,
0.025, 0.025, 0.025, 13, 1100, 170)
I apologize for not being word-perfect in English.
Thank you.