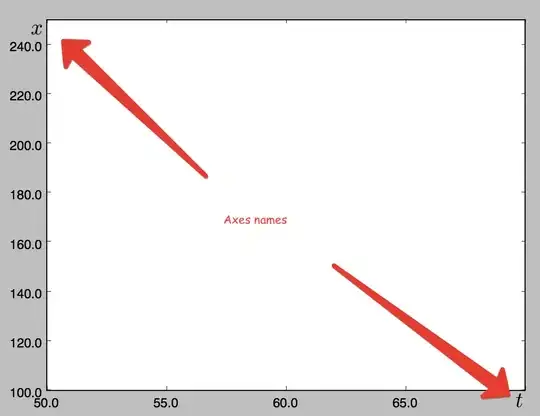
I have a grid of circular data, e.g. the data is given by its angle from 0 to π. Within this data, I have another smaller grid.
This might look like this:
What I want to do is to interpolate the black data on the red dots. Therefore I'm using scipy.interpolate.griddata. This will give me the following result:
As you see, there is a discontinuity when the angle changes from 'almost 0' to 'almost π'.
To remove that, I tried to unwrap the data before interpolation. According to this answer (here). And I get this (better) result, but surprisingly, there is a new disconituity on the right that I don't understand.
So my question is: How to use np.unwrap to get a continous interpolation? Or is there a better way to do so?
Here is the code to reproduce:
import numpy as np
from matplotlib import pyplot as plt
from scipy.interpolate import griddata
ax = plt.subplot()
ax.set_aspect(1)
# Simulate some given data.
x, y = np.meshgrid(np.linspace(-10, 10, 20), np.linspace(-10, 10, 20))
phi = np.arctan2(y, x) % (2 * np.pi)
data = np.arctan2(np.cos(phi), np.sin(phi)) % np.pi
# Plot data.
u = np.cos(data)
v = np.sin(data)
ax.quiver(x, y, u, v, headlength=0.01, headaxislength=0, pivot='middle', units='xy')
# Create a smaller grid within.
x1, y1 = np.meshgrid(np.linspace(-6, 5, 20), np.linspace(-4, 8, 25))
# ax.plot(x1, y1, '.', color='red', markersize=2)
# Prepare data.
data = np.unwrap(2 * data) / 2
# Interpolate data on grid.
interpolation = griddata((x.flatten(), y.flatten()), data.flatten(), (x1.flatten(), y1.flatten()))
# Plot interpolated data.
u1 = np.cos(interpolation)
v1 = np.sin(interpolation)
ax.quiver(x1, y1, u1, v1, headlength=0.01, headaxislength=0, pivot='middle', units='xy',
scale=3, width=0.03, color='red')
plt.show()