What is the fastest way to reverse a power of two in C?

Question

In the equation :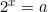

What is the fastest way in C language to find x with a given power of two value (a) ?

Edit :

1. The mathematical exact solution is :
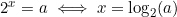
2. As (a) is a positive integer and a power of two (no rational number, no equal to zero), this problem can be simplified as "looking for position of set bit".
3. This post is focused on lite embedded CPU systems. For example : ARM CORTEX M4.

---

a to x results :

  a | x
 -------
  1 | 0
  2 | 1
  4 | 2
  8 | 3
 16 | 4
 32 | 5
 64 | 6
128 | 7
256 | 8
512 | 9
...

---

Option 1 : The dirty loop

unsigned int get_power_of_two_exponent(unsigned int value)
{
    unsigned int x = 0;

    while( ( 1 << x ) != value)
    {
        x ++;
    }

return x;
}

---

Option 2 : The weird trick

#include <stdint.h>

#if defined(__GNUC__)
static int highest_bit_set(uint32_t value)
{
    if (sizeof (unsigned int) == sizeof value)
        return 31 - __builtin_clz(value);
    else
    if (sizeof (unsigned long) == sizeof value)
        return 31 - __builtin_clzl(value);
    else
        exit(127); /* Weird architecture! */
}
#endif

---

Any faster options ?

Answer 1

Fastest in C is almost always look-up tables, at the expense of memory use. Assuming that the value is always exactly a power of 2, you can make a look-up table like this:

uint8_t get_exponent (uint8_t val)
{
  static const uint8_t byte[256] = 
  {
    [1]   = 0,
    [2]   = 1,
    [4]   = 2,
    [8]   = 3,
    [16]  = 4,
    [32]  = 5,
    [64]  = 6,
    [128] = 7,
  };

  return byte[val & 0xFF];
}

It will return 0 in case you pass a value which isn't a power of 2.

This can be expanded further either by looping through for example the 4 bytes of a uint32_t and do 4 table-lookups. Or by making even bigger look-up tables.

On x86 I get the above to boil down to this tiny, branch-free machine code:

get_exponent:
        movzx   edi, dil
        movzx   eax, BYTE PTR byte.2173[rdi]
        ret

(Swapping to uint_fast8_t gives identical code in this case.)

Answer 2

This answer is in dispute - see comment.

The fastest way, somewhat facetiously¹, is to write

switch (a)
{
    case 1: return 0;
    case 2: return 1;
    case 4: return 2;
    ...

Clearly there are as many labels as there are bits in the type, but this is still O(1).

You could even truncate a to a power of two using the idiom a ^ (a & (a - 1)), at the expense of portability given that only works if a is a 2's complement type.

---

¹Although in C++ you could get the compiler to build the table with constexpr and metaprogramming techniques.

Answer 3

The best performances (on my embedded ARM CORTEX M4 CPU core) are obtained with :

Builtin CLZ solution (Count Leading Zero’s)

Moreover, the CLZ solution is by far much more memory efficient than the lookup table method which take the second place.

Often, the LookUp table method still less efficient than the Builtin CLZ because the table is stored in RAM like a DDR for example. Thus, it can takes a dozen of cycle to access the data in this kind of RAM. In this example, this is amplified by the fact that the instruction cache is enabled but not the data cache. Besides, having this huge table stored in cache would not have been very appropriate.

Answer 4

It depends how big values you would like to search, and if there's the biggest possible input defined.

If x can be, for example, 100, searching from beginning (x = 0) with step x++, isn't elegant and optimized (100 checks). You can set step x+=5. If the result is lower than searched value, x+=5. If bigger - step back with x-- (max 4 Times). Size of step you can adjust to your needs.

If there's a "top-limit", you can create an array of possible x and implement binary search.

Answer 5

@Lundin's answer seems the best in terms of speed (just 3 assembly instructions!), but it may not be a good option for your embedded system. If huge LUTs are not an option:

The weird trick seems to be the a fast option, I guess (you should benchmark each option and see actual results, though). You could use that one in case it exists, and fallback to the usual shifting otherwise:

#include <stdint.h>


static int get_pow2_exp(uint32_t value)
{

#if defined(__GNUC__)
        if (sizeof(unsigned int) == sizeof(value))
                return 31 - __builtin_clz(value);
        if (sizeof(unsigned long) == sizeof(value))
                return 31 - __builtin_clzl(value);
#endif
        int x;

        for (x = -1; value; value >>= 1)
                x++;

        return x;
}

If you want to ensure that it is a power of two, you may use popcnt. Your while loop is an infinite loop in case the input is not a power of two, while mine just gives a solution based on the highest bit (which may be incorrect, depending on your needs).

Answer 6

2^x = a is the equation

Assuming 32 bit architecture and 'a' & 'x' as integers.

Here is my approach

uint32_t x;
uint8_t *ptr ;
uint8_t ByteNo,BitNo,i;

void My_Function(uint32_t a)
{
    ByteNo = BitNo = 9;//some random number
    ptr = (uint8_t*)&a;//Assuming points to LSB in variable a
    for(i=0;i<4;i++)
    {
        switch(*ptr)
        {
        case 0x01:  BitNo=0;break;
        case 0x02:  BitNo=1;break;
        case 0x04:  BitNo=2;break;
        case 0x08:  BitNo=3;break;
        case 0x10:  BitNo=4;break;
        case 0x20:  BitNo=5;break;
        case 0x40:  BitNo=6;break;
        case 0x80:  BitNo=7;break;
        case 0x00:  BitNo=9;break;
        default :   break;//take care error condition
        }

        if(9 != BitNo)
        {
            break;
        }
        else
        {
            ptr++;
        }
    }//for loop
    ByteNo = i;

    x = (BitNo) + (ByteNo*8);

}//My_Function

Another approach:

switch(a)
{
case   0x00000001:   x=0;   break;
case   0x00000002:   x=1;   break;
case   0x00000004:   x=2;   break;
case   0x00000008:   x=3;   break;
case   0x00000010:   x=4;   break;
case   0x00000020:   x=5;   break;
case   0x00000040:   x=6;   break;
case   0x00000080:   x=7;   break;
case   0x00000100:   x=8;   break;
case   0x00000200:   x=9;   break;
case   0x00000400:   x=10;   break;
case   0x00000800:   x=11;   break;
case   0x00001000:   x=12;   break;
case   0x00002000:   x=13;   break;
case   0x00004000:   x=14;   break;
case   0x00008000:   x=15;   break;
case   0x00010000:   x=16;   break;
case   0x00020000:   x=17;   break;
case   0x00040000:   x=18;   break;
case   0x00080000:   x=19;   break;
case   0x00100000:   x=20;   break;
case   0x00200000:   x=21;   break;
case   0x00400000:   x=22;   break;
case   0x00800000:   x=23;   break;
case   0x01000000:   x=24;   break;
case   0x02000000:   x=25;   break;
case   0x04000000:   x=26;   break;
case   0x08000000:   x=27;   break;
case   0x10000000:   x=28;   break;
case   0x20000000:   x=29;   break;
case   0x40000000:   x=30;   break;
case   0x80000000:   x=31;   break;
default:    break;//error condition
}