The Wikipedia article on color difference is worth reading, and so is the article on a “low-cost approximation” by CompuPhase linked therein. I will base my attempt on the latter.
You didn't specify a language, so I'll write it in not optimized Python (except for the integer optimizations already present in the reference article), in order for it to be readily translatable into other languages.
n_colors = 25
n_global_moves = 32
class Color:
max_weighted_square_distance = (((512 + 127) * 65025) >> 8) + 4 * 65025 + (((767 - 127) * 65025) >> 8)
def __init__(self, r, g, b):
self.r, self.g, self.b = r, g, b
def weighted_square_distance(self, other):
rm = (self.r + other.r) // 2 # integer division
dr = self.r - other.r
dg = self.g - other.g
db = self.b - other.b
return (((512 + rm) * dr*dr) >> 8) + 4 * dg*dg + (((767 - rm) * db*db) >> 8)
def min_weighted_square_distance(self, index, others):
min_wsd = self.max_weighted_square_distance
for i in range(0, len(others)):
if i != index:
wsd = self.weighted_square_distance(others[i])
if min_wsd > wsd:
min_wsd = wsd
return min_wsd
def is_valid(self):
return 0 <= self.r <= 255 and 0 <= self.g <= 255 and 0 <= self.b <= 255
def add(self, other):
return Color(self.r + other.r, self.g + other.g, self.b + other.b)
def __repr__(self):
return f"({self.r}, {self.g}, {self.b})"
colors = [Color(127, 127, 127) for i in range(0, n_colors)]
steps = [Color(dr, dg, db) for dr in [-1, 0, 1]
for dg in [-1, 0, 1]
for db in [-1, 0, 1] if dr or dg or db] # i.e., except 0,0,0
moved = True
global_move_phase = False
global_move_count = 0
while moved or global_move_phase:
moved = False
for index in range(0, len(colors)):
color = colors[index]
if global_move_phase:
best_min_wsd = -1
else:
best_min_wsd = color.min_weighted_square_distance(index, colors)
for step in steps:
new_color = color.add(step)
if new_color.is_valid():
new_min_wsd = new_color.min_weighted_square_distance(index, colors)
if best_min_wsd < new_min_wsd:
best_min_wsd = new_min_wsd
colors[index] = new_color
moved = True
if not moved:
if global_move_count < n_global_moves:
global_move_count += 1
global_move_phase = True
else:
global_move_phase = False
print(f"n_colors: {n_colors}")
print(f"n_global_moves: {n_global_moves}")
print(colors)
The colors are first set all to grey, i.e., put in the center of the RGB color cube, and then moved in the color cube in such a way as to hopefully maximize the minimum distance between colors.
To save CPU time the square of the distance is used instead of the distance itself, which would require the calculation of a square root.
Colors are moved one at a time, by a maximum of 1 in each of the 3 directions, to one of the adjacent colors that maximizes the minimum distance from the other colors. By so doing, the global minimum distance is (approximately) maximized.
The “global move” phases are needed in order to overcome situations where no color would move, but forcing all colors to move to a position which is not much worse than their current one causes the whole to find a better configuration with the subsequent regular moves. This can best be seen with 3 colors and no global moves, modifying the weighted square distance to be simply rd*rd+gd*gd+bd*bd: the configuration becomes
[(2, 0, 0), (0, 253, 255), (255, 255, 2)]
while, by adding 2 global moves, the configuration becomes the expected one
[(0, 0, 0), (0, 255, 255), (255, 255, 0)]
The algorithm produces just one of several possible solutions. Unfortunately, since the metric used is not Euclidean, it's not possible to simply flip the 3 dimension in the 8 possible combinations (i.e., replace r→255-r and/or the same for g and/or b) to get equivalent solutions. It's probably best to introduce randomness in the order the color moving steps are tried out, and vary the random seed.
I have not corrected for the monitor's gamma, because its purpose is precisely that of altering the spacing of the brightness in order to compensate for the eyes' different sensitivity at high and low brightness. Of course, the screen gamma curve deviates from the ideal, and a (system dependent!) modification of the gamma would yield better results, but the standard gamma is a good starting point.
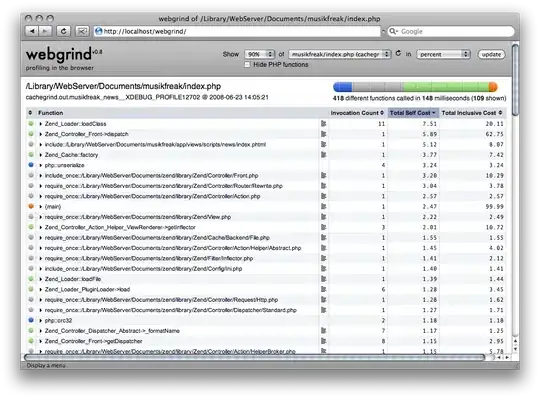
This is the output of the algorithm for 25 colors:

Note that the first 8 colors (the bottom row and the first 3 colors of the row above) are close to the corners of the RGB cube (they are not at the corners because of the non-Euclidean metric).