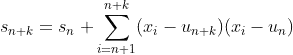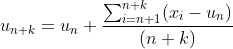What's the formula for Welford's Algorithm for Variance/Std with Batch Updates?

Question

I want to extend Welford's online algorithm to be able to be updated with multiple numbers (in batch) instead of just one at a time: https://en.wikipedia.org/wiki/Algorithms_for_calculating_variance

I tried to update the algorithm from the wiki page like this:

# my attempt.
def update1(existingAggregate, newValues):
    (count, mean, M2) = existingAggregate
    count += len(newValues) 
    delta = np.sum(np.subtract(newValues, [mean] * len(newValues)))
    mean += delta / count
    delta2 = np.sum(np.subtract(newValues, [mean] * len(newValues)))
    M2 += delta * delta2

    return (count, mean, M2)

# The original two functions from wikipedia.
def update(existingAggregate, newValue):
    (count, mean, M2) = existingAggregate
    count += 1 
    delta = newValue - mean
    mean += delta / count
    delta2 = newValue - mean
    M2 += delta * delta2

def finalize(existingAggregate):
    (count, mean, M2) = existingAggregate
    (mean, variance, sampleVariance) = (mean, M2/count, M2/(count - 1)) 
    if count < 2:
        return float('nan')
    else:
        return (mean, variance, sampleVariance)

However, I must not understand it correctly, because the result is wrong:

# example x that might have led to an a = (2, 2.0, 2.0).
x = [1.0, 3.0]
mean = np.mean(x)
count = len(x)
m2 = np.sum(np.subtract(x, [mean] * count)**2)

a = (count, mean, m2)
print(a)
# new batch of values.
b = [5, 3]

Note that a = (2, 2.0, 2.0) means that we had 2 observations, and their mean was 2.0.

# update one at a time.
temp = update(a, newValues[0])
result_single = update(temp, newValues[1])
print(finalize(result_single))

# update with my faulty batch function.
result_batch = update1(a, newValues)
print(finalize(result_batch))

The correct output should be the one from applying the single number update twice:

(3.0, 2.0, 2.6666666666666665)
(3.0, 2.5, 3.3333333333333335)

What am I missing regarding the correct variance updates? Do I need to update the finalize function as well somehow?

The reason I need to do this, is because I am working with extremely large monthly files (with varying numbers of observations) and I need to get to yearly means and variances.

Answer 1

Thanks to Nico's clarification's I figured it out! The problem was that I summed for the deltas and then multiply to get M2, but instead have to sum over the product of the deltas. Here is the correct batch function that is able to accept single numbers as well as batches:

# https://en.wikipedia.org/wiki/Algorithms_for_calculating_variance
def update(existingAggregate, newValues):
    if isinstance(newValues, (int, float, complex)):
        # Handle single digits.
        newValues = [newValues]

    (count, mean, M2) = existingAggregate
    count += len(newValues) 
    # newvalues - oldMean
    delta = np.subtract(newValues, [mean] * len(newValues))
    mean += np.sum(delta / count)
    # newvalues - newMeant
    delta2 = np.subtract(newValues, [mean] * len(newValues))
    M2 += np.sum(delta * delta2)

    return (count, mean, M2)

def finalize(existingAggregate):
    (count, mean, M2) = existingAggregate
    (mean, variance, sampleVariance) = (mean, M2/count, M2/(count - 1)) 
    if count < 2:
        return float('nan')
    else:
        return (mean, variance, sampleVariance)

Sample Usage:

x = [1.0, 3.0]
mean = np.mean(x)
count = len(x)
m2 = np.sum(np.subtract(x, [mean] * count)**2)

a = (count, mean, m2)
print(a)
# new batch of values.
b = [5, 3]

result_batch = update(a, b)
result_batch1 = update(a, b[0])

print(finalize(result_batch))
print(finalize(result_batch1))

And it is indeed faster:

import timeit
x = random.sample(range(1, 10000), 1000)
# ...
b = random.sample(range(1, 10000), 1000)

start_time = timeit.default_timer()
result_batch = update(a, b)
print(f'{timeit.default_timer() - start_time:.4f}')
print(*(f'{x:.2f}' for x in finalize(result_batch)))

start_time = timeit.default_timer()
for i in b:
    a  = update1(a, i)
print(f'{timeit.default_timer() - start_time:.4f}')
print(*(f'{x:.2f}' for x in finalize(result_batch)))

Result:

0.0010
5008.36 8423224.68 8427438.40
0.0031
5008.36 8423224.68 8427438.40

Answer 2

I am not too familiar with Python, so I will rather stick to a mathematical notation.

To update the mean, you have to do:

s = sum of new values
c = number of new values
newMean = oldMean + sum_i (newValue[i] - oldMean) / newCount

For M2, you have to add another summation:

newM2 = oldM2 + sum_i ((newValue[i] - newMean) * (newValue[i] - oldMean))

I am not sure if you actually save anything with this bulk update as you still have a loop inside.

Answer 3

Adding to the previous answer, the derivation for the generalized case (calculate s_{n+k} given s_n) follows similarly to the proof for the k=1 version, and gives:

Where u_{n+k} is also calculated batch-wise via:

You can also consider an approach base on computing the mean/variance of c = A union B from the mean/variance of A and B, that is easily parallelizable (Chan's algorithm).