I suspect you have a math problem, not a code problem.
The math
The intersection points are where 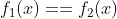 , with f1, f2 "defined" by
, with f1, f2 "defined" by 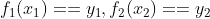
Why scare quotes around "defined"? Well, that defines the functions over the sampling points of your inputs, but there is no guarantee that the intersection is one of those. So you need to somehow guess what the function is equal to between sampling points; that's a problem of interpolation, which can be anywhere from "trivial" to "writing a PhD about the optimal way to do it".
I will assume in your case a linear interpolant will do (draw straight lines between data points). In that case, there is an intersection point in the segment between consecutive datapoints whenever  changes sign between those datapoints.
changes sign between those datapoints.
The code
In your exact case, one of the function is a constant: 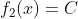 , which simplifies the solution. (If it was not the case, you would have to walk along segments of each curve and check for intersections; that can be done in linear time (of the sum of both arrays' lengths) but it takes a bit more coding.)
, which simplifies the solution. (If it was not the case, you would have to walk along segments of each curve and check for intersections; that can be done in linear time (of the sum of both arrays' lengths) but it takes a bit more coding.)
import matplotlib.pyplot as plt
import numpy as np
def find_intersections(x, y, C):
# Contains numpy indexing tricks that can be hard to reproduce
# in the case where both functions are non-constants
ii, = np.nonzero((y[1:]-C)*(y[:-1]-C) < 0.) # intersection indices
x_intersections = x[ii] + (C - y[ii])/(y[1+ii] - y[ii])*(x[1+ii] - x[ii])
y_intersections = C * np.ones(len(ii))
return x_intersections, y_intersections
# parabolic data for example
x1 = np.linspace(-2., 2)
y1 = x1 ** 2
C = 2.0
x2 = np.asarray([min(x1), max(x1)])
y2 = np.asarray([C, C])
xint, yint = find_intersections(x1, y1, C)
plt.figure()
plt.plot(x1, y1)
plt.plot(x2, y2)
plt.plot(xint, yint, 'ro')
plt.show()
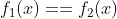 , with f1, f2 "defined" by
, with f1, f2 "defined" by 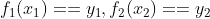
 changes sign between those datapoints.
changes sign between those datapoints.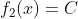 , which simplifies the solution. (If it was not the case, you would have to walk along segments of each curve and check for intersections; that can be done in linear time (of the sum of both arrays' lengths) but it takes a bit more coding.)
, which simplifies the solution. (If it was not the case, you would have to walk along segments of each curve and check for intersections; that can be done in linear time (of the sum of both arrays' lengths) but it takes a bit more coding.)