A square can be defined as the triple {center1, side, angle} where center = {double center.x, double center.y} is the center of the square, double side is the length of the side of the square, and finally double angle is the angle to which the square is rotated from the horizontal direction.
Given the two squares, you can represent them as
square1 = {center1, side1, angle1} and square2 = {center2, side2, angle2}. The idea for an algorithm is:
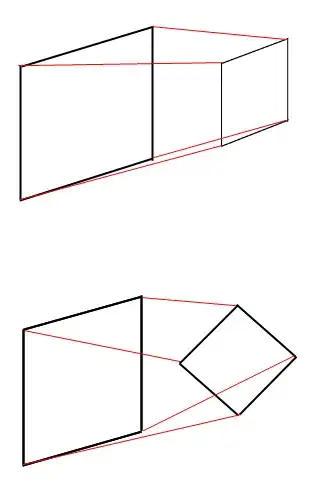
Step 1: rotate square2 by angle - angle1 so that its sides are parallel to the coordinate axes, as in your first example. Obtain the new
square1 ---> sqare10 = {center1, side1, 0}
Step 2: rotate square2 also by angle - angle1. Obtain the new square
square2 ---> sqare20 = {center2, side2, angle2 - angle1}
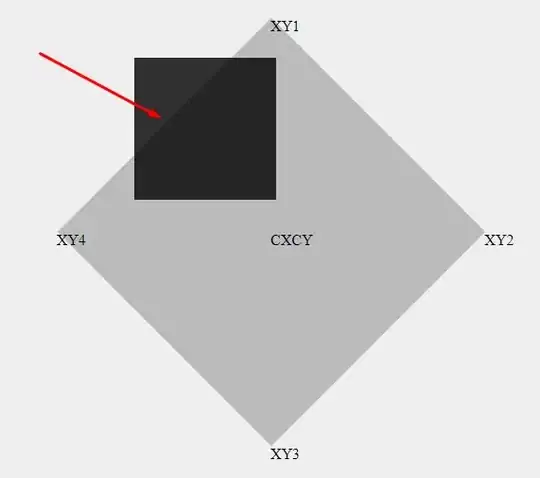
Step 3: introduce the new square square30 = {center2, side3, 0} so that this new square is the smallest square that contains sqare20 and its sides are parallel to the coordinate axes (the four vertices of square20 lie on the edges of square30 and the two of them share the same center). Square30's side-length is calculated as
side3 = side2 * (cos(angle2 - angle1) + sin(angle2 - angle1))
Step 4: Now you are in the situation of your first example where the pair of squares
square10 and square30 have edges parallel to the coordinate axes. Check the relative position of these two squares: square10 and square30:
if square30 is completely inside square10 then the original square2 is completely inside the original square1
else if square30 has an edge that touches an edge of square10, then the original square2 has a vertex that touches on of the sides of the original square1