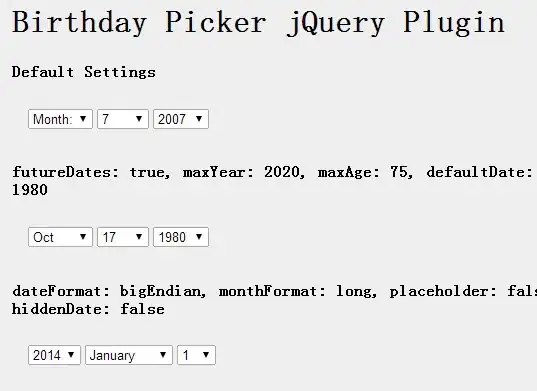
Solving a system of mass, spring, damper and Coulomb friction

Question

Consider the system below:

            
        Fig.1 - Mass, spring, damper and Coulomb frction (image courtesy of Wikimedia).

with a dynamic equation of:

where Ff is the Amontons-Columb friction defined as:

and consequently, the no-slip condition is defined as

Following this example, I have a vague code in mind which I don't know how to complete:

from scipy.integrate import odeint
import numpy as np

m = 1.0
k = 2.0
c = 0.1
mus = 0.3
muk = 0.2
g = 9.8
vf = 0.01

def eq(X, t, Xi):
  Ff = k * (Xi[0] - X[0]) + c * (Xi[1] - X[1]) # - m * dydt

  if np.abs(X[1]) < vf and np.abs(Ff) < mus * m * g :
    Ff = k * (Xi[0] - X[0]) + c * (Xi[1] - X[1]) # - m * dydt
  else:
    Ff = -np.sign(X[1]) * muk * m * g
    pass

  dxdt = X[1]
  dydt = (k * (Xi[0] - X[0]) + c * (Xi[1] - X[1]) - Ff) / m
  return [dxdt, dydt]

t = np.linspace(0, 10, 1000)
Xi0 = np.piecewise(t, [t < 1, t >= 1], [0, 1])
X0 = [0, 0]
sol = odeint(eq, X0, t)

where Xi0 is a step function. My main issue is that when I want to define Ff it depends on dydt which is to be defined later in that scope!

I would appreciate if you could help me know what is the most canonical way to numerically solve this system. Thanks in advance.

I am not sure the given expression of `F_f` is correct. Do you have a source for this? Often solid friction is considered in a static system. It's actually more a question about physics than python code... I would say that the dynamic equation needs to be solved only in case of slippage, otherwise the equation is dX/dt=(acceleration=0, velocity=0)... — xdze2, Jun 26 '19 at 10:51
I think I have implemented it correctly in the below posts. the code in this post had some issues. — Foad S. Farimani, Jun 26 '19 at 10:54
@Foad If the implementations in the answers below are better than the ones in the question, please edit the question to include them (or a shorter version of them, etc) — Itamar Mushkin, Aug 26 '19 at 12:10

score 0 · Answer 1 · answered Jun 25 '19 at 14:59

I'm gonna put a simplified/temporary solution here till someone comes with a better one:

from scipy.integrate import odeint
import numpy as np
import matplotlib.pyplot as plt

m = 0.2
k = 2.0
c = 0.1
mus = 0.3
muk = 0.2
g = 9.8
vf = 0.01
v0 = 0.0
t1 = 10
sign = lambda x: np.tanh(100*x)

def Xi(t):
  if t < 1 :
    return 0
  else:
    return 1

vXi = np.vectorize(Xi)

def eq(X, t, Xi):
  Ff = k * (Xi(t) - X[0])

  if np.abs(X[1]) < vf and np.abs(Ff) < mus * m * g :
    Ff = k * (Xi(t) - X[0])
  else:
    Ff = sign(X[1]) * muk * m * g

  d2x = (k * (Xi(t) - X[0]) - Ff) / m
  return [X[1], d2x]

t = np.linspace(0, t1, 1000)
X0 = [v0, 0]
sol = odeint(func = eq, y0 = X0, t = t, args = (Xi, ), mxstep = 50000, atol = 1e-5)

plt.plot(t, sol[:, 0], 'r-', label = 'Output (x(t))')
plt.plot(t, vXi(t), 'b-', label = 'Input (xi(t))')
plt.ylabel('values')
plt.xlabel('time')
plt.legend(loc='best')
plt.show()

and the result is:

I used this, this and this posts to write the code. I ignored damping and inertia to simplify the problem.

score 0 · Answer 2 · edited Jun 20 '20 at 09:12

another approach is just to use a for loop and calculate steps sequentially:

Y = np.piecewise(t, [t < t2, t >= t2], [0, 1])
dY = np.insert(np.diff(Y) / np.diff(t), 0 , v0, axis = 0)
X = np.zeros((steps,))
dX = np.zeros((steps,))
dX[0] = v0
ddX = np.zeros((steps,))
Ff = np.zeros((steps,))
# FS = np.zeros((steps,))
dt = t1 / (steps - 1)

for ii in range(1, steps):
  X[ii] = X[ii - 1] + dt * dX[ii - 1]
  dX[ii] = dX[ii - 1] + dt * ddX[ii - 1]
  Ff[ii] = k * (Y[ii] - X[ii]) #+ c * (dY[ii] - dX[ii])
  if not (np.abs(dX[ii]) < vf and np.abs(Ff[ii]) < mus * m * g) :
    Ff[ii] = np.sign(dX[ii]) * muk * m * g
  ddX[ii] = (k * (Y[ii] - X[ii]) - Ff[ii]) / m

the result is shown as green in below plot:

I also changed the vf to 0.001. The results are different from odeint for some reason!

score 0 · Answer 3 · answered Jun 29 '21 at 11:42

Writing the equations of such a system is not obvious. And solving it is also not easy.

If the Python constraint can be released, I would suggest using OpenModelica to solve this problem. In the modelica library of components, you have the element

.Modelica.Mechanics.Translational.Components.MassWithStopAndFriction

which can be used to model dry friction.

Solving a system of mass, spring, damper and Coulomb friction

3 Answers3

Linked