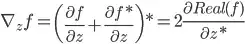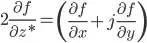5

I am working with complex-valued neural networks.

For Complex-valued neural networks Wirtinger calculus is normally used. The definition of the derivate is then (take into acount that functions are non-Holomorphic because of Liouville's theorem):

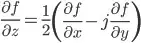
wirtinger

If you take Akira Hirose book "Complex-Valued Neural Networks: Advances and Applications", Chapter 4 equation 4.9 defines:

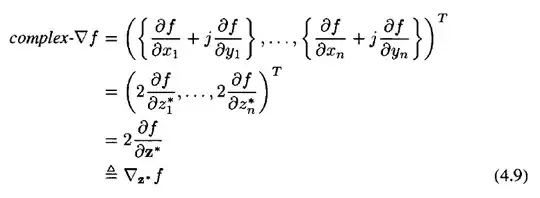
Screenshot from 2020-03-03 10-38-21

Where the partial derivative is also calculated using Wirtinger calculus of course.

Is this the case for tensorflow? or is it defined in some other way? I cannot find any good reference on the topic.

J Agustin Barrachina
  • 3,501
  • 1
  • 32
  • 52
  • 1
    I don't know much (or anything) about complex analysis, but maybe if you can give some examples of non-holomorphic functions we can look up what TensorFlow does about the gradient. While TF does support complex tensors, I'm not sure to what extent gradients are implemented for them (for simple arithmetic it seems to work, but I don't know about more complicated operations). Even if a function is regarded as "non-differentiable" by TensorFlow, you could implement the gradient yourself with `tf.gradient` (but that's probably not what you're interested in now). – jdehesa Jul 19 '19 at 09:26

1 Answers1

0

Ok, so I discussed this in an existing thread in github/tensorflow and @charmasaur found the response, the equation used by Tensorflow for the gradient is:

tf-grad-def

When using the definition of the partial derivatives wrt z and z* it uses Wirtinger Calculus.

For cases of a real-valued scalar function of one or several complex variables, this definitions becomes:

Which is indeed the definition used in Complex-Valued Neural Networks (CVNN) applications (In this applications, the function is the loss/error function which is indeed real).

J Agustin Barrachina
  • 3,501
  • 1
  • 32
  • 52
  • I have untagged this as the solution because I still need a verifiable source/reference I can cite. I would like a reference that asserts this is the equation for Tensorflow or someone within Tensorflow that works with this that tells me it is indeed correct. – J Agustin Barrachina Mar 02 '20 at 16:12
  • Also asked for that [here](https://github.com/tensorflow/tensorflow/issues/3348#issuecomment-593483897) – J Agustin Barrachina Mar 02 '20 at 16:21