Rationals are enumerable. For example this code finds k-th rational in open interval 0..1, with ordering that {n1, d1} is before {n2, d2} if (d1<d2 || (d1==d2 && n1<n2)) assuming {n,d} is coprime.
RankedRational[i_Integer?Positive] :=
Module[{sum = 0, eph = 1, den = 1},
While[sum < i, sum += (eph = EulerPhi[++den])];
Select[Range[den - 1], CoprimeQ[#, den] &][[i - (sum - eph)]]/den
]
In[118]:= Table[RankedRational[i], {i, 1, 11}]
Out[118]= {1/2, 1/3, 2/3, 1/4, 3/4, 1/5, 2/5, 3/5, 4/5, 1/6, 5/6}
Now I would like to generate random rationals, given an upper bound on the denominator sort-of uniformly, so that for large enough denominator rationals will be uniformly distributed over the unit interval.
Intuitively, one could pick among all rationals with small denominators with equal weights:
RandomRational1[maxden_, len_] :=
RandomChoice[(Table[
i/j, {j, 2, maxden}, {i,
Select[Range[j - 1], CoprimeQ[#, j] &]}] // Flatten), len]
Can one generate random rationals with this distribution more efficiently, without constructing all of them ? It does not take much for this table to become huge.
In[197]:= Table[RankedRational[10^k] // Denominator, {k, 2, 10}]
Out[197]= {18, 58, 181, 573, 1814, 5736, 18138, 57357, 181380}
Or maybe it is possible to efficiently generate rationals with bounded denominator having a different "feels-like-uniform" distribution ?
EDIT This is Mathematica code which runs acceptance-rejection generation suggested by btilly.
Clear[RandomFarey];
RandomFarey[n_, len_] := Module[{pairs, dim = 0, res, gcds},
Join @@ Reap[While[dim < len,
gcds = cfGCD[pairs = cfPairs[n, len - dim]];
pairs = Pick[pairs, gcds, 1];
If[pairs =!= {},
dim += Length@Sow[res = pairs[[All, 1]]/pairs[[All, 2]]]];
]][[2, -1]]
]
The following compiled function generations pairs of integers {i,j} such that 1<=i < j<=n:
cfPairs =
Compile[{{n, _Integer}, {len, _Integer}},
Table[{i, RandomInteger[{i + 1, n}]}, {i,
RandomChoice[2 (n - Range[n - 1])/(n (n - 1.0)) -> Range[n - 1],
len]}]];
and the following compiled function computes gcd. It assumes the input is a pair of positive integers.
cfGCD = Compile[{{prs, _Integer, 1}}, Module[{a, b, p, q, mod},
a = prs[[1]]; b = prs[[2]]; p = Max[a, b]; q = Min[a, b];
While[q > 0, mod = Mod[p, q]; p = q; q = mod]; p],
RuntimeAttributes -> Listable];
Then
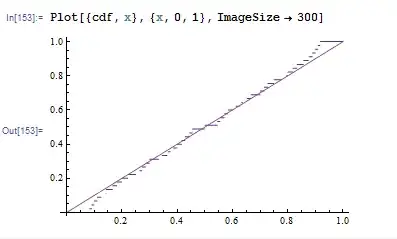
In[151]:= data = RandomFarey[12, 10^6]; // AbsoluteTiming
Out[151]= {1.5423084, Null}
In[152]:= cdf = CDF[EmpiricalDistribution[data], x];
In[153]:= Plot[{cdf, x}, {x, 0, 1}, ImageSize -> 300]