9

If I give Mathematica the input

TreeForm[Unevaluated[4^5]]

I expect to see three boxes -- power, 4, and 5.

Instead I see a single box with 1024. Can anyone explain?

William Jockusch
  • 26,513
  • 49
  • 182
  • 323

2 Answers2

19

A level of Unevaluated is stripped off with every evaluation, so you can get what you want with:

TreeForm[Unevaluated@Unevaluated[4^5]]

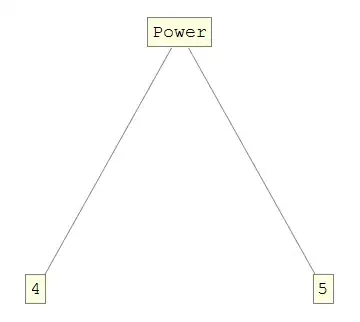
enter image description here

Mr.Wizard
  • 24,179
  • 5
  • 44
  • 125
  • 6
    I think the situation is more subtle than it may appear from this solution. If we try `f[Unevaluated[4^5]]` with some generic undefined `f`, we get the same back (as we should). `Unevaluated` is equivalent to a temporary `Hold*` - attribute for, in this case, `TreeForm`. What happens to the argument then, is determined by `TreeForm` internals.The fact that one layer of `Unevaluated` is not enough, reveals something that may perhaps be qualified as evaluation leak in the implementation of `TreeForm` - apparently it evaluates the passed expression once somewhere inside its implementation. – Leonid Shifrin Apr 20 '11 at 10:18
  • 6
    Continuing... But then, there is no way to know how many levels of Unevaluated we my need, if any. In some other cases (other built-ins) we may need just one level, as the OP expected. In other words, IMO this aspect of the behavior or `TreeForm` is rather puzzling and unintuitive (to me, I join the OP here), and the solution with many levels of `Unevaluated` reveals certain specifics about the internals of `TreeForm`, and, while totally valid, should have a status of a workaround tailored specifically at `TreeForm`, rather than a general solution for similar cases with other built-ins. – Leonid Shifrin Apr 20 '11 at 10:26
  • 1
    @Leonid Just as an example `FullForm[Unevaluated[4^5]]` works as expected – Dr. belisarius Apr 20 '11 at 12:29
  • 6
    @belisarius Your example is rather special, because `FullForm` is special - it is not a normal function in some ways, see my comments to this post: http://stackoverflow.com/questions/4851948/return-equality-from-mathematica-function/4854542#4854542 . But we can make a very simple experiment: `f[x_] := Hold[x]; f[Unevaluated[4^5]]` will return `Hold[4^5]`. The fact that we need 2 levels of `Unevaluated` for `TreeForm` means that `TreeForm` does one extra internal evaluation of the input argument, while IMO it should not, as it is given all it needs to know. I'd consider this a borderline bug. – Leonid Shifrin Apr 20 '11 at 13:25
  • @Leonid **ALL** other _xxxForm_ commands show Unevaluated[ ] as a head. It's not only a _FullForm[ ]_ issue – Dr. belisarius Apr 20 '11 at 14:21
  • @belisarius I did not mean specifically `FullForm` - all these *xxxForm* must be special (as compared to other built-in or user-defined functions), in this sense. – Leonid Shifrin Apr 20 '11 at 14:26
9

Compare 

TreeForm@Unevaluated[4^5]

enter image description here

with 

TreeForm@Hold[4^5]

enter image description here

From the help:

Unevaluated[expr] represents the unevaluated form of expr when it appears as the argument to a function.

and

Hold[expr] maintains expr in an unevaluated form.

so, as Unevaluated[4^5] gets to TreeForm ... it gets evaluated ...

It works like this: 

f[x_+y_]:=x^y;
f[3+4]
(*
-> f[7]
*)
f[Unevaluated[3+4]]
(*
->81
*)
Dr. belisarius
  • 60,527
  • 15
  • 115
  • 190