How to calculate bounce angle?

Question

I played around with it for a while, but I simply can't figure it out.

I made a tank that fires missiles, and when the missiles hit the walls, I want them to bounce off, but I want them to bounce off to the right angle.

Right now I haven't got any obstacles, the missiles just bounce off when they get outside the viewportRectangle I made.

Is the solution I'm looking for quite advanced?

Is there a relativly simple way to do it?

Answer 1

You might think that because your walls are aligned with the coordinate axes that it makes sense to write special case code (for a vertical wall, negate the x-coordinate of the velocity; for a horizontal wall, negate the y-coordinate of the velocity). However, once you've got the game working well with vertical and horizontal walls, probably the next thing you'll think is, "what about walls at arbitrary angles?" So it's worth thinking about the general case from the beginning.

In the general case, suppose your missile has velocity v and hits a wall with surface normal n.

Split v into components u perpendicular to the wall and w parallel to it.

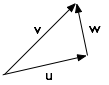
Where:

u = (v · n / n · n) n
w = v − u

Here, v · n is the dot product of the vectors v and n. See the link for an explanation of how to compute it. The dot product n · n evaluates to the square of the length of the normal vector; if you always keep your normals in the form of unit vectors then n · n = 1 and you can omit the division.

After bouncing, the component of motion parallel to the wall is affected by friction f, and the component perpendicular to the wall is affected by elasticity, which can be given in the form of a coefficient of restitution r.

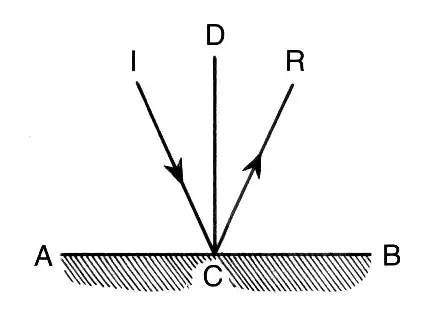
So the velocity after the collision is v′ = f w − r u. In a perfectly elastic, frictionless collision, v′ = w − u; that is, the motion is reflected about the normal at the point of collision, as in the diagram given in Bill's answer.

This approach works just the same in three dimensions too.

(Obviously this is a very simplified notion of bouncing; it takes no account of angular momentum or deformation. But for many kinds of video games this kind of simplification is perfectly adequate.)

Answer 2

I think an easier way to do this is to use the velocity of the missile instead of calculating angles. Say you have a missile that has xVelocity and yVelocity to represent its movement horizontally and vertically. Those velocities can be positive or negative to represent left, right, up, or down.

• If a missile hits a top or bottom border reverse the sign of the yVelocity.
• If a missile hits a left or right border reverse the sign of the xVelocity.

This will keep the movement in the opposite axis the same.

Borrowing the image from ChrisF's answer, let's say the missile starts out at position I.

With the xVelocity and yVelocity both being positive (in 2D graphics right and down are typically positive) the missile will travel in the direction indicated. Let's just assign values of

xVelocity = 3
yVelocity = 4

When the missile hits the wall at position C, its xVelocity shouldn't change, but its yVelocity should be reversed to -4 so that it travels back in the up direction, but keeps going to the right.

The benefit to this method is that you only need to keep track of a missile's xPosition, yPosition, xVelocity, and yVelocity. Using just these four components and your game's update rate, the missile will always get redrawn at the correct position. Once you get into more complicated obstacles that are not at straight angles or are moving, it will be a lot easier to work with X and Y velocities than with angles.

Answer 3

I've had this problem, the only way I found was separating the axes of collision!

Try it:

x += velocity * Math.cos(angle * Math.PI /180);
y += velocity * Math.sin(angle * Math.PI /180);

if (x < 0 || x > canvas.width) {
     angle = 180 - angle;   
}
else if (y < 0 ||y > canvas.height) {
     angle = 360 - angle; 
}

I hope this helps you!

Answer 4

For perfect particles (& light) the angle of reflection is equal to the angle of incidence, as illustrated by this diagram (from commons.wikimedia.org).

The Wikipedia page on reflection is quite good at explaining how it works.

It's a little bit more complicated when you take into account the elasticity and materials of the object and the obstacles, but this is probably good enough for most applications.

Answer 5

As an aside to the specific physics question you are asking, I would recommend the book "Beginning Math and Physics for Game Programmers" by Wendy Stahler. I found it quite useful for my game/physics programming projects.

The code that accompanies the book is C++ but if you know C#, it would be pretty easy to make the conversion.

Have a good one!

Answer 6

180-a will not work in all instances, unless you are merely working a bounce on a top surface when X is increasing.

One direction to head is the XNA forums or pick up XNA sample code. It is C# and it is for building games. I am not stating you want to build your games in XNA, but it is a great tool, and it is free.

Answer 7

a = 2w - b

where:
a => resulting angle
w => wall or floor or ceiling angle
b => ball angle

This is what I come up after trying to find the simplest formula for computing just the resulting angle of ball bouncing the walls, ceiling and floor. The result could go beyond +360 or -360 degrees but they are still equivalent angle.

For example if the ceiling angle is 270deg and the ball angle is 30deg, the resulting angle is 510deg which is equivalent to +150deg or -210 deg. If you'll use 90deg for the ceiling instead of 270deg, the result is still 150deg.

Answer 8

Not complicated at all - pseudo-code:

angleObjectHitWall = a;
bounceAngle = 180-a;

Of course this is a very simple calculation, and is totally irrelevant once you start to take into account factors such as material, gravity, walls which aren't straight, etc...

Answer 9

This is really a physics question, so if you are not a physicist (and since you are asking this question, I'm going to take it that you are not) it will require a lot of reading and brainstorming to get it right.

I suggest reading this wikipedia entry to get the basic idea about the depth of your question.

If you only want to make it "look plausible" then I wouldn't worry about it too much and use Bill the Lizard's answer, however if you want to make it right you will have quite an adventure. Don't let this scare you tho! Good luck!

Answer 10

if(!Collide(Missle, Mainchar)){
(Velocity.x)*-1;
(Velocity.y)*-1;
}

It works and is simple, good luck.