13

I would like to draw a circular graph of nodes where certain nodes have a link between them. Here are a few examples from social network graphs:

example1
(source: wrightresult.com)

example2

example3
(source: twit88.com)

How can this be done with MATLAB? Is it possible without installing a separate package?

Glorfindel
  • 21,988
  • 13
  • 81
  • 109
Vass
  • 2,682
  • 13
  • 41
  • 60
  • possible duplicate of [How to visualize correlation matrix as a schemaball in Matlab](http://stackoverflow.com/questions/17038377/how-to-visualize-correlation-matrix-as-a-schemaball-in-matlab) – Shai Jun 13 '13 at 19:05

2 Answers2

13

Here is one way you can do what you want. First, generate points on the circle that you are interested in

clear;
theta=linspace(0,2*pi,31);theta=theta(1:end-1);
[x,y]=pol2cart(theta,1);

Next, if you know the pairs of nodes that are connected, you can skip this step. But in many cases, you get a connectivity matrix from other computations, and you find the indices of the connected nodes from that. Here, I've created a Boolean matrix of connections. So, if there are N nodes, the connectivity matrix is an NxN symmetric matrix, where if the i,jth element is 1, it means you have a connection from node i to node j and 0 otherwise. You can then extract the subscripts of the non-zero pairs to get node connections (only the upper triangle is needed).

links=triu(round(rand(length(theta))));%# this is a random list of connections
[ind1,ind2]=ind2sub(size(links),find(links(:)));

This is the connectivity matrix I generated with the code above.

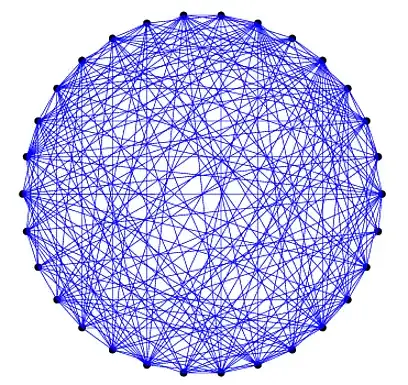
enter image description here

Now we just need to plot the connections, one at a time

h=figure(1);clf(h);
plot(x,y,'.k','markersize',20);hold on
arrayfun(@(p,q)line([x(p),x(q)],[y(p),y(q)]),ind1,ind2);
axis equal off

which will give you a figure similar to your examples

enter image description here

abcd
  • 41,765
  • 7
  • 81
  • 98
  • 3
    Nice, but your call to [ARRAYFUN](http://www.mathworks.com/help/techdoc/ref/arrayfun.html) is unnecessary. If you enter matrices for the X and Y data, functions like [PLOT](http://www.mathworks.com/help/techdoc/ref/plot.html) and [LINE](http://www.mathworks.com/help/techdoc/ref/line.html) will automatically plot one line per column. So you can plot the connections like so: `plot([x(ind1); x(ind2)],[y(ind1); y(ind2)],'b');` – gnovice Apr 27 '11 at 15:52
  • 2
    @gnovice: yes, I'm aware of that. I used `arrayfun` because I wasn't sure if the OP was just going to lift the plotting commands and use directly in his program or follow the entire code here. If he had initialized his node vectors & connection indices as the transpose of what I have here, and just used plotting functions from SO, using `plot()` may result in a single connected line that's all over the place, instead of a line per pair, whereas `arrayfun` will still do it pair-by-pair. But yes, if OP is consistent with his vectors, `plot()` is the way to go. – abcd Apr 27 '11 at 16:09
5

Inspired by the latest blog post by Cleve Moler, you could also use the gplot function to draw a graph given an adjacency matrix and node coordinates.

Here is an example using bucky; a demo function part of MATLAB that generates the graph of a truncated icosahedron (looks like a soccer ball). We will only use its adjacency matrix for this example since we are laying out the vertices in a circular shape:

%# 60-by-60 sparse adjacency matrix
A = bucky();
N = length(A);

%# x/y coordinates of nodes in a circular layout
r =  1;
theta = linspace(0,2*pi,N+1)'; theta(end) = [];
xy = r .* [cos(theta) sin(theta)];

%# labels of nodes
txt = cellstr(num2str((1:N)','%02d'));

%# show nodes and edges
line(xy(:,1), xy(:,2), 'LineStyle','none', ...
    'Marker','.', 'MarkerSize',15, 'Color','g')
hold on
gplot(A, xy, 'b-')
axis([-1 1 -1 1]); axis equal off
hold off

%# show node labels
h = text(xy(:,1).*1.05, xy(:,2).*1.05, txt, 'FontSize',8);
set(h, {'Rotation'},num2cell(theta*180/pi))

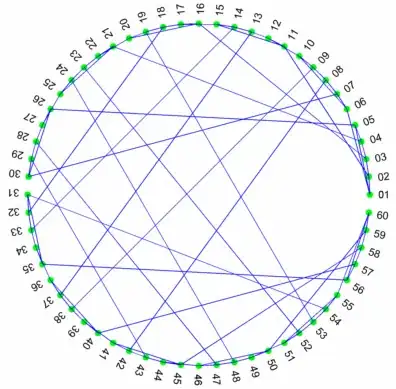
circular_graph

We can take this a step further and try to minimize edge crossings. That is we want to rearrange the nodes so that the edges are as close as possible to the circumference of the circle.

This can be done by finding a symmetric permutation of the matrix that minimizes its bandwidth (non-zeros are closer to the diagonal)

matrix_permutation

p = symrcm(A);
A = A(p,p);
txt = txt(p);

The result in this case:

circular_graph_permutation

Other improvements include replacing straight lines with curved splines to draw the edges, (that way you get a nicer graph similar to the second one you've shown), or using different colors to show clusters of vertices and their edges (obviously you'll need to do graph clustering). I will leave those steps to you :)

Amro
  • 123,847
  • 25
  • 243
  • 454