0

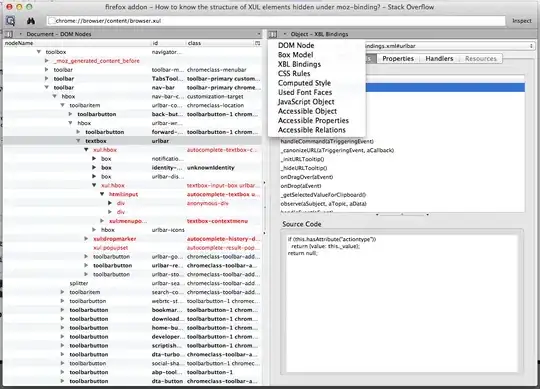
I'm trying to fit some count data for the number of fish purchased by anglers(grey in the image) with a distribution using optim in R. I've fit both a poisson (red) and negative binomial distribution (blue) but as you can see neither seems to be right. What should my next steps be for getting a better fit?

My graph:

enter image description here

#fit poisson curve to data using optim
minus.logL.s<-function(lambda, dat){
  -sum(dpois(dat,lambda, log=TRUE))}

mle<-optim(par=45,fn=minus.logL.s, method="BFGS",hessian=T,dat=survey.responses.baitusers$fish.per.trip)
mle

#simulate data coming from a poisson distribution of mean 38
simspois<-as.data.frame(rpois(1000, 38)) 
colnames(simspois)<-("simulated_values")

#fit negative binomial curve
minus.logL.nb<-function(pars, dat){
  mu<-pars[1]
  size<-pars[2]
  -sum(dnbinom(dat, mu=mu, size=size,log=TRUE))}

mlenb<-optim(par=c(mu=38,size=1),fn=minus.logL.nb, method="BFGS",hessian=T,dat=survey.responses.baitusers$fish.per.trip)
mlenb

simsnegbin<-as.data.frame(rnbinom(1000,size=4, mu=38))
colnames(simsnegbin)<-("simulated_valuesnb")

#graph both
graph<-ggplot(survey.responses.baitusers)+aes(fish.per.trip)+geom_histogram()+geom_smooth(data=simspois, aes(simulated_values), stat = "count",color="red")+geom_smooth(data=simsnegbin, aes(simulated_valuesnb), stat="count", color="blue")
graph

Output from negative binomial fitting:

$par
       mu      size 
38.333338  4.107287

Output from poisson fitting:

$par
[1] 38.33333

My data:

> survey.responses.baitusers$fish.per.trip
  [1]  15  34  42  38   8  38  21  29  58  29  40  35  33  51  50  40   8  45  44  45  34  57   8  28  63  54  22  44  65  54  54  15  12
 [34]  42  59  40  43  95  80  15  54  19  44  27  53  95  21  38  40  13  25  27  79  38  85  40  33  74  34  77  34  34  33  35  89  34
 [67]  34  37  16  60  17  21  18  37  34  27  30  62  48  35  55  50  23  32  56  34  11  21  34  48  15  34  26  54   8  95   8  58  54
[100]  44  34  47  35  13  21  53  52  52  40  40  33   8  15  15  25  41  63  34  38  87  14  68  58  59  34  55  24  24  35  33  21   8
[133]   8  15  51  48   8  21  39  29  50  54  62  16  54  33  58  22  49  40  30  51  21  19  51  40  34  27  40  45  80  69   8  42  33
[166]  62  40  82  17  14  30  61  45  70  33  33  16  49  32  34  31  31  18  64  33  39  21  56  40  52  71  34  30  27  54   8  64  16
[199]  54 127  13  51  40  33  63  31  30  63  56  57  77  46  64  22  34  50  66  33  34  59  45  16  21  60  58  15  64  29  40  44  29
[232]   8  21  16  72  34  49  57  34  34  15  33  54  40  32  33  95 107  49  64  59  64  37  70  45  16  16  40  19  53  34  39  21  36
[265]  34  17   8  34  51  13  20  34  21  38  36  36  41  34  83  27   8  45  29  34  21  37  44  15  50  25  27   8  27  19  24  40   8
[298]  28  36  24  40  21  70  20  34  21  46  16  20   8  33  34  54  44  77  80  15  34  40  29  48  59  29   8  15  47  45  21  41  23
[331]  34  51  14  40  25  45  64  59 107  21  59  27  56  48  34  45  59  35  30  37  32   8  51  11  48  64  32   8  52  14  20  18   8
[364]  53  52  53  33  34  48  62  34  34   8  46  39  21  33  34  40  49  52  19  24  29  43  19  29  27  46  52  29  51  61  16  17  35
[397]  34  40  25  28  34  42  66  35  49  35  51  66  21  51  45  14  53  22  42  64   8  48  28  66  52  40  29  34  34  41  59  34  52
[430]  16  32  20  35   8   8  21  49  40  33  16  24   8  42  23  63  26  21  33   8  23 112  57   8  46  18  67  34  30  33  40  43  57
[463]  60  33  14  27  44  21  31  30  27  49  57  69  66  22  28  55  11  43
Rui Barradas
  • 70,273
  • 8
  • 34
  • 66
Meg McEachran
  • 31
  • 1
  • 3
  • 1
    This is probably a better question at [stats.se] since it's more about the statistics than the code. It would also be helpful to have that sample of data in a workable format, such as from `dput`, since we can't copy & paste that and easily use it in R – camille Sep 27 '19 at 20:08
  • Thanks for the tip! How does dput work? I knew there was probably a better way to provide the data but didn't know what it was. – Meg McEachran Sep 27 '19 at 20:32
  • Take a look at https://stackoverflow.com/questions/5963269/how-to-make-a-great-r-reproducible-example, should be examples there – camille Sep 27 '19 at 20:39
  • 1
    I agree that a question that is specific to distributions could be a better fit for Cross Validated. Since it appears as though you have a lower limit to the number of fish purchases, you may be looking for a truncated distribution. Zero-truncated distributions are what I see most often for count distributions. – aosmith Sep 27 '19 at 20:57

0 Answers0