As the original data is not available I generated some test data. The approach is as follows. If the data is a set of plateaus with jumps, checking the standard deviation on a moving window, will give peaks at jumps. With a threshold isolate the peaks. Get an estimate for the jump by looking at the data after applying a moving average. This provides a good starting point for fitting. As fit function I use once again my favourite tanh.
The result looks as follows:
import matplotlib.pyplot as plt
import numpy as np
from operator import itemgetter
from itertools import groupby
from scipy.optimize import leastsq
def moving_average( data, windowsize, **kwargs ):
mode=kwargs.pop('mode', 'valid')
weight = np.ones( windowsize )/ float( windowsize )
return np.convolve( data, weight, mode=mode)
def moving_sigma( data, windowsize ):
l = len( data )
sout = list()
for i in range( l - windowsize + 1 ):
sout += [ np.std( data[ i : i + windowsize ] ) ]
return np.array( sout )
def m_step( x, s, x0List, ampList, off ):
assert len( x0List ) == len( ampList )
out = [ a * 0.5 * ( 1 + np.tanh( s * (x - x0) ) ) for a, x0 in zip( ampList, x0List )]
return sum( out ) + off
def residuals( params, xdata, ydata ):
assert not len(params) % 2
off = params[0]
s = params[1]
rest = params[2:]
n = len( rest )
x0 = rest[:n/2]
am = rest[n/2:]
diff = [ y - m_step( x,s, x0, am, off ) for x, y in zip( xdata, ydata ) ]
return diff
### generate data
np.random.seed(776)
a=0
data = list()
for i in range(15):
a = 50 * ( 1 - 2 * np.random.random() )
for _ in range ( np.random.randint( 5, 35 ) ):
data += [a]
xx = np.arange( len( data ), dtype=np.float )
noisydata = list()
for x in data:
noisydata += [ x + np.random.normal( scale=5 ) ]
###define problem specific parameters
myWindow = 10
thresh = 8
cutoffscale = 1.1
### data treatment
avdata = moving_average( noisydata, myWindow )
avx = moving_average( xx, myWindow )
sdata = moving_sigma( noisydata, myWindow )
### getting start values for the fit
seq = [x for x in np.where( sdata > thresh )[0] ]
# from https://stackoverflow.com/a/3149493/803359
jumps = [ map( itemgetter(1), g ) for k, g in groupby( enumerate( seq ), lambda ( i, x ) : i - x ) ]
xjumps = [ [ avx[ k ] for k in xList ] for xList in jumps ]
means = [ np.mean( x ) for x in xjumps ]
### the delta is too small as one only looks above thresh so lets increase it by guessing
deltas = [ ( avdata[ x[-1] ] - avdata[ x[0] ] ) * cutoffscale for x in jumps ]
guess = [ avdata[0], 2] + means + deltas
### fitting
sol, err = leastsq( residuals, guess, args=( xx, noisydata ), maxfev=10000 )
fittedoff = sol[0]
fitteds = sol[1]
fittedx0 = sol[ 2 : 2 + len( means ) ]
fittedam = sol[ 2 + len( means ) : ]
### plotting
fig = plt.figure()
ax = fig.add_subplot( 1, 1, 1 )
# ~ ax.plot( data )
ax.plot( xx, noisydata, label='noisy data' )
ax.plot( avx, avdata, label='moving average' )
ax.plot( avx, sdata, label='window sigma' )
for j in means:
ax.axvline( j, c='#606060', linestyle=':' )
yy = [ m_step( x, 2, means, deltas, avdata[0] ) for x in xx]
bestyy = [ m_step( x, fitteds, fittedx0, fittedam, fittedoff ) for x in xx ]
ax.plot( xx, yy, label='guess' )
ax.plot( xx, bestyy, label='fit' )
plt.legend( loc=0 )
plt.show()
Which gives the following graph:
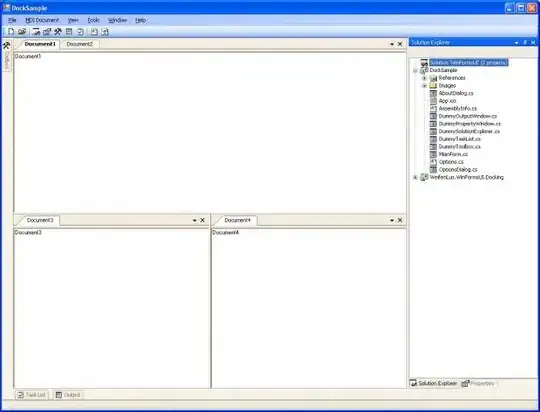
Some smaller jumps are not detected, but it should be clear that this is expected. Moreover, the entire process is not very fast. Due to the threshold, the initial guess get worse to larger x the more jumps are present. Finally, a sequence of small jumps is not detected such that a resulting slope in the data is fitted as one large plateau with an obvious large error. One could introduce an additional check for this and add positions for jumps to fit accordingly.
Also notice that the choice of the window size determines down to which distance two jumps will be detected as individual ones.