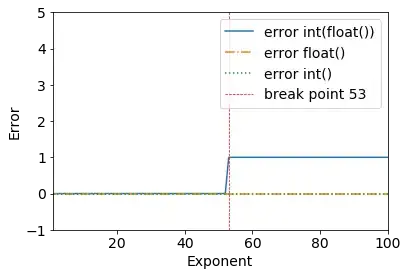
I've got this error recently:
>>> (2**53+1) - int(float(2**53+1))
1
>>> (2**53) - int(float(2**53))
0
Can someone help me understand why exactly int(float(2**53)) == int(float(2**53+1)) would be true? i.e. Why I get this 1 error?
Just added an answer to Is floating point math broken? if anyone is interested. Thanks to @a_guest