Counterclockwise sorting of x, y data

Question

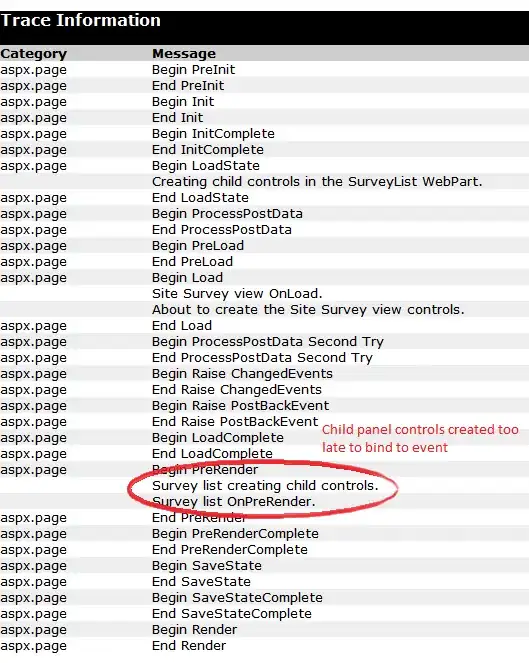
I have a set of points in a text file: random_shape.dat. The initial order of points in the file is random. I would like to sort these points in a counter-clockwise order as follows (the red dots are the xy data):

I tried to achieve that by using the polar coordinates: I calculate the polar angle of each point (x,y) then sort by the ascending angles, as follows:

"""
Script: format_file.py
Description: This script will format the xy data file accordingly to be used with a program expecting CCW order of data points, By soting the points in Counterclockwise order
Example: python format_file.py random_shape.dat
"""

import sys
import numpy as np

# Read the file name
filename = sys.argv[1]

# Get the header name from the first line of the file (without the newline character)
with open(filename, 'r') as f:
    header = f.readline().rstrip('\n')

angles = []
# Read the data from the file
x, y = np.loadtxt(filename, skiprows=1, unpack=True)


for xi, yi in zip(x, y):
    angle = np.arctan2(yi, xi) 
    if angle < 0:
        angle += 2*np.pi # map the angle to 0,2pi interval
    angles.append(angle)

# create a numpy array 
angles = np.array(angles)

# Get the arguments of sorted 'angles' array
angles_argsort = np.argsort(angles)

# Sort x and y
new_x = x[angles_argsort]
new_y = y[angles_argsort]

print("Length of new x:", len(new_x))
print("Length of new y:", len(new_y))

with open(filename.split('.')[0] + '_formatted.dat', 'w') as f:
    print(header, file=f)
    for xi, yi in zip(new_x, new_y):
        print(xi, yi, file=f)

print("Done!")

By running the script:

python format_file.py random_shape.dat

Unfortunately I don't get the expected results in random_shape_formated.dat! The points are not sorted in the desired order.

Any help is appreciated.

EDIT: The expected resutls:

• Create a new file named: filename_formatted.dat that contains the sorted data according to the image above (The first line contains the starting point, the next lines contain the points as shown by the blue arrows in counterclockwise direction in the image).

EDIT 2: The xy data added here instead of using github gist:

random_shape
0.4919261070361315  0.0861956168831175
0.4860816807027076  -0.06601587301587264
0.5023029456281289  -0.18238249845392662
0.5194784026079869  0.24347943722943777
0.5395164357511545  -0.3140611471861465
0.5570497147514262  0.36010146103896146
0.6074231036252226  -0.4142604617604615
0.6397066014669927  0.48590810704447085
0.7048302091822873  -0.5173701298701294
0.7499157837544145  0.5698170011806378
0.8000108666123336  -0.6199254449254443
0.8601249660418364  0.6500974025974031
0.9002010323281716  -0.7196585989767801
0.9703341483292582  0.7299242424242429
1.0104102146155935  -0.7931355765446666
1.0805433306166803  0.8102046438410078
1.1206193969030154  -0.865251869342778
1.1907525129041021  0.8909386068476981
1.2308285791904374  -0.9360074773711129
1.300961695191524  0.971219008264463
1.3410377614778592  -1.0076702085792988
1.4111708774789458  1.051499409681228
1.451246943765281  -1.0788793781975592
1.5213800597663678  1.1317798110979933
1.561456126052703  -1.1509956709956706
1.6315892420537896  1.2120602125147582
1.671665308340125  -1.221751279024005
1.7417984243412115  1.2923406139315234
1.7818744906275468  -1.2943211334120424
1.8520076066286335  1.3726210153482883
1.8920836729149686  -1.3596340023612745
1.9622167889160553  1.4533549783549786
2.0022928552023904  -1.4086186540731989
2.072425971203477  1.5331818181818184
2.1125020374898122  -1.451707005116095
2.182635153490899  1.6134622195985833
2.2227112197772345  -1.4884454939000387
2.292844335778321  1.6937426210153486
2.3329204020646563  -1.5192876820149541
2.403053518065743  1.774476584022039
2.443129584352078  -1.5433264462809912
2.513262700353165  1.8547569854388037
2.5533387666395  -1.561015348288075
2.6234718826405867  1.9345838252656438
2.663547948926922  -1.5719008264462806
2.7336810649280086  1.9858362849271942
2.7737571312143436  -1.5750757575757568
2.8438902472154304  2.009421487603306
2.883966313501766  -1.5687258953168035
2.954099429502852  2.023481896890988
2.9941754957891877  -1.5564797323888229
3.0643086117902745  2.0243890200708385
3.1043846780766096  -1.536523022432113
3.1745177940776963  2.0085143644234558
3.2145938603640314  -1.5088557654466737
3.284726976365118  1.9749508067689887
3.324803042651453  -1.472570838252656
3.39493615865254  1.919162731208186
3.435012224938875  -1.4285753640299088
3.5051453409399618  1.8343467138921687
3.545221407226297  -1.3786835891381335
3.6053355066557997  1.7260966810966811
3.655430589513719  -1.3197205824478546
3.6854876392284703  1.6130086580086582
3.765639771801141  -1.2544077134986225
3.750611246943765  1.5024152236652237
3.805715838087476  1.3785173160173163
3.850244800627849  1.2787337662337666
3.875848954088563  -1.1827449822904361
3.919007794704616  1.1336638361638363
3.9860581363759846  -1.1074537583628485
3.9860581363759846  1.0004485329485333
4.058012891753723  0.876878197560016
4.096267318663407  -1.0303482880755608
4.15638141809291  0.7443374218374221
4.206476500950829  -0.9514285714285711
4.256571583808748  0.6491902794175526
4.3166856832382505  -0.8738695395513574
4.36678076609617  0.593855765446675
4.426894865525672  -0.7981247540338443
4.476989948383592  0.5802489177489183
4.537104047813094  -0.72918339236521
4.587199130671014  0.5902272727272733
4.647313230100516  -0.667045454545454
4.697408312958435  0.6246979535615904
4.757522412387939  -0.6148858717040526
4.807617495245857  0.6754968516332154
4.8677315946753605  -0.5754260133805582
4.917826677533279  0.7163173947264858
4.977940776962782  -0.5500265643447455
5.028035859820701  0.7448917748917752
5.088149959250204  -0.5373268398268394
5.138245042108123  0.7702912239275879
5.198359141537626  -0.5445838252656432
5.2484542243955445  0.7897943722943728
5.308568323825048  -0.5618191656828015
5.358663406682967  0.8052154663518301
5.41877750611247  -0.5844972451790631
5.468872588970389  0.8156473829201105
5.5289866883998915  -0.6067217630853987
5.579081771257811  0.8197294372294377
5.639195870687313  -0.6248642266824076
5.689290953545233  0.8197294372294377
5.749405052974735  -0.6398317591499403
5.799500135832655  0.8142866981503349
5.859614235262157  -0.6493565525383702
5.909709318120076  0.8006798504525783
5.969823417549579  -0.6570670995670991
6.019918500407498  0.7811767020857934
6.080032599837001  -0.6570670995670991
6.13012768269492  0.7562308146399057
6.190241782124423  -0.653438606847697
6.240336864982342  0.7217601338055886
6.300450964411845  -0.6420995670995664
6.350546047269764  0.6777646595828419
6.410660146699267  -0.6225964187327819
6.4607552295571855  0.6242443919716649
6.520869328986689  -0.5922077922077915
6.570964411844607  0.5548494687131056
6.631078511274111  -0.5495730027548205
6.681173594132029  0.4686727666273125
6.7412876935615325  -0.4860743801652889
6.781363759847868  0.3679316979316982
6.84147785927737  -0.39541245791245716
6.861515892420538  0.25880333951762546
6.926639500135833  -0.28237987012986965
6.917336127605076  0.14262677798392165
6.946677533279001  0.05098957832291173
6.967431210462995  -0.13605442176870675
6.965045730326905  -0.03674603174603108

Answer 1

I find that an easy way to sort points with x,y-coordinates like that is to sort them dependent on the angle between the line from the points and the center of mass of the whole polygon and the horizontal line which is called alpha in the example. The coordinates of the center of mass (x0 and y0) can easily be calculated by averaging the x,y coordinates of all points. Then you calculate the angle using numpy.arccos for instance. When y-y0 is larger than 0 you take the angle directly, otherwise you subtract the angle from 360° (2). I have used numpy.where for the calculation of the angle and then numpy.argsort to produce a mask for indexing the initial x,y-values. The following function sort_xy sorts all x and y coordinates with respect to this angle. If you want to start from any other point you could add an offset angle for that. In your case that would be zero though.

def sort_xy(x, y):

    x0 = np.mean(x)
    y0 = np.mean(y)

    r = np.sqrt((x-x0)**2 + (y-y0)**2)

    angles = np.where((y-y0) > 0, np.arccos((x-x0)/r), 2*np.pi-np.arccos((x-x0)/r))

    mask = np.argsort(angles)

    x_sorted = x[mask]
    y_sorted = y[mask]

    return x_sorted, y_sorted

Plotting x, y before sorting using matplotlib.pyplot.plot (points are obvisously not sorted):

Plotting x, y using matplotlib.pyplot.plot after sorting with this method:

Answer 2

Counter-clock-wise order depends on the choice of a pivot point. From your question, one good choice of the pivot point is the center of mass.

Something like this:

# Find the Center of Mass: data is a numpy array of shape (Npoints, 2)
mean = np.mean(data, axis=0)
# Compute angles
angles = np.arctan2((data-mean)[:, 1], (data-mean)[:, 0])
# Transform angles from [-pi,pi] -> [0, 2*pi]
angles[angles < 0] = angles[angles < 0] + 2 * np.pi
# Sort
sorting_indices = np.argsort(angles)
sorted_data = data[sorting_indices]

Answer 3

If it is certain that the curve does not cross the same X coordinate (i.e. any vertical line) more than twice, then you could visit the points in X-sorted order and append a point to one of two tracks you follow: to the one whose last end point is the closest to the new one. One of these tracks will represent the "upper" part of the curve, and the other, the "lower" one.

The logic would be as follows:

dist2 = lambda a,b: (a[0]-b[0])*(a[0]-b[0]) + (a[1]-b[1])*(a[1]-b[1])

z = list(zip(x, y)) # get the list of coordinate pairs
z.sort() # sort by x coordinate

cw = z[0:1] # first point in clockwise direction
ccw = z[1:2] # first point in counter clockwise direction
# reverse the above assignment depending on how first 2 points relate
if z[1][1] > z[0][1]: 
    cw = z[1:2]
    ccw = z[0:1]

for p in z[2:]:
    # append to the list to which the next point is closest
    if dist2(cw[-1], p) < dist2(ccw[-1], p):
        cw.append(p)
    else:
        ccw.append(p)

cw.reverse()
result = cw + ccw

This would also work for a curve with steep fluctuations in the Y-coordinate, for which an angle-look-around from some central point would fail, like here:

No assumption is made about the range of the X nor of the Y coordinate: like for instance, the curve does not necessarily have to cross the X axis (Y = 0) for this to work.

Answer 4

If:

• the shape is arbitrarily complex and
• the point spacing is ~random

then I think this is a really hard problem.

For what it's worth, I have faced a similar problem in the past, and I used a traveling salesman solver. In particular, I used the LKH solver. I see there is a Python repo for solving the problem, LKH-TSP. Once you have an order to the points, I don't think it will be too hard to decide on a clockwise vs clockwise ordering.

Answer 5

Not really a python question I think, but still I think you could try sorting by - sign(y) * x doing something like:

def counter_clockwise_sort(points):
    return sorted(points, key=lambda point: point['x'] * (-1 if point['y'] >= 0 else 1))

should work fine, assuming you read your points properly into a list of dicts of format {'x': 0.12312, 'y': 0.912}

EDIT: This will work as long as you cross the X axis only twice, like in your example.

Answer 6

If we want to answer your specific problem, we need to pick a pivot point.

Since you want to sort according to the starting point you picked, I would take a pivot in the middle (x=4,y=0 will do).

Since we're sorting counterclockwise, we'll take arctan2(-(y-pivot_y),-(x-center_x)) (we're flipping the x axis).

We get the following, with a gradient colored scatter to prove correctness (fyi I removed the first line of the dat file after downloading):

import numpy as np
import matplotlib.pyplot as plt
points = np.loadtxt('points.dat')

#oneliner for ordering points (transform, adjust for 0 to 2pi, argsort, index at points)
ordered_points = points[np.argsort(np.apply_along_axis(lambda x: np.arctan2(-x[1],-x[0]+4) + np.pi*2, axis=1,arr=points)),:]

#color coding 0-1 as str for gray colormap in matplotlib
plt.scatter(ordered_points[:,0], ordered_points[:,1],c=[str(x) for x in np.arange(len(ordered_points)) / len(ordered_points)],cmap='gray')

Result (in the colormap 1 is white and 0 is black), they're numbered in the 0-1 range by order:

Answer 7

For points with comparable distances between their neighbouring pts, we can use KDTree to get two closest pts for each pt. Then draw lines connecting those to give us a closed shape contour. Then, we will make use of OpenCV's findContours to get contour traced always in counter-clockwise manner. Now, since OpenCV works on images, we need to sample data from the provided float format to uint8 image format. Given, comparable distances between two pts, that should be pretty safe. Also, OpenCV handles it well to make sure it traces even sharp corners in curvatures, i.e. smooth or not-smooth data would work just fine. And, there's no pivot requirement, etc. As such all kinds of shapes would be good to work with.

Here'e the implementation -

import numpy as np
import matplotlib.pyplot as plt
from scipy.spatial.distance import pdist
from scipy.spatial import cKDTree
import cv2
from scipy.ndimage.morphology import binary_fill_holes

def counter_clockwise_order(a, DEBUG_PLOT=False):
    b = a-a.min(0)
    d = pdist(b).min()
    c = np.round(2*b/d).astype(int)

    img = np.zeros(c.max(0)[::-1]+1, dtype=np.uint8)

    d1,d2 = cKDTree(c).query(c,k=3)
    b = c[d2]
    p1,p2,p3 = b[:,0],b[:,1],b[:,2]
    for i in range(len(b)):    
        cv2.line(img,tuple(p1[i]),tuple(p2[i]),255,1)
        cv2.line(img,tuple(p1[i]),tuple(p3[i]),255,1)

    img = (binary_fill_holes(img==255)*255).astype(np.uint8)   
    if int(cv2.__version__.split('.')[0])>=3:
        _,contours,hierarchy = cv2.findContours(img.copy(),cv2.RETR_TREE,cv2.CHAIN_APPROX_NONE)
    else:
        contours,hierarchy = cv2.findContours(img.copy(),cv2.RETR_TREE,cv2.CHAIN_APPROX_NONE)

    cont = contours[0][:,0]        
    f1,f2 = cKDTree(cont).query(c,k=1)
    ordered_points = a[f2.argsort()[::-1]]

    if DEBUG_PLOT==1:
        NPOINTS = len(ordered_points)
        for i in range(NPOINTS):
            plt.plot(ordered_points[i:i+2,0],ordered_points[i:i+2,1],alpha=float(i)/(NPOINTS-1),color='k')
        plt.show()
    return ordered_points

Sample run -

# Load data in a 2D array with 2 columns
a = np.loadtxt('random_shape.csv',delimiter='  ')
ordered_a = counter_clockwise_order(a, DEBUG_PLOT=1)

Output -

Answer 8

A bit late to the game, but I had a similar issue that couldn't use the center of mass concept due to a lot of over hangs/undercuts in the data. Similar to Divakar's answer I used spacing between points to do the sorting, but with just Pandas. The idea is to calculate the distance between one point and all other data points. The data point with shortest distance would be considered to be the next neighbor.

The implementation looks like this:

import pandas as pd
import matplotlib.pyplot as plt
import numpy as np

df = pd.read_csv('data.csv', headers=None)

#  Creating blank lists for XY data
x = []
y = []

# Creating list with first entry being the desired starting point
l=[[df.iloc[0][0],df.iloc[1][0]]]

# Creating dataframe that does not contain the starting point
df2=df.iloc[1:]

# Iterating through each data point
for i in l:
    # Once the list reaches the same length as the original dataframe the
    # process has examined all data points and breaks
    if len(l) == len(df):
        break

    else:
        # Calculating the distance to each point
        d = np.sqrt((df2[0]-i[0])**2+(df2[1]-i[1])**2)
    
        # Removing any duplicates to the current point
        dd = d[d!=0]
    
        # Setting a minimum distance threshold for the points,
        # helps to deal with noisy data and should be adjusted to your data
        if d.min()<5:        
        
            # Adding the sorted X & Y data to lists for easy plotting
            x.append(df2.loc[dd.idxmin()][0])
            y.append(df2.loc[dd.idxmin()][1])
       
            # Adding the next data point for analysis to the list
            l.append([df2.loc[dd.idxmin()][0],df2.loc[dd.idxmin()][1]])
        
            # Removing the current datapoint from the dataframe to prevent
            # multiple analysis
            df2=df2.drop(index=dd.idxmin())

# plotting the sorted data
plt.plot(x,y)
plt.scatter(x,y,c='r')

Plotting the original data looks like this: Raw Data

The sorted data now looks like this: Sorted Data

I found this method to be really useful for images of interfaces that can have a lot of overlapping features like this image of a wave:

Wave Image

When turning this into XY coordinates using a program like ImageJ the plotted data looks like this:

Raw Wave XY Data

Using this method successfully sorts the data so you get this:

Sorted Wave XY Data