0

I am trying to find the average time complexity for the Fibonacci series using mathematical approach.

The best case is O(1), while the worst case is O(2^n). The Average case can be found by dividing the sum of times of all cases by the number of cases.

So, I believe that the average case can be found like this(using the sum of geometric series):

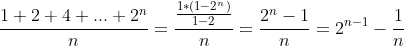
Thus, it should be still O(2^n) . Can you please tell me if my calculations and approach are correct?

The sample code for the Fibonacci() is shown below.

def Fibonacci(n): 
    if n==1: 
        return 0
    elif n==2: 
        return 1
    else: 
        return Fibonacci(n-1)+Fibonacci(n-2)
Alex.Kh
  • 572
  • 7
  • 15
  • How did you get the geometric series for the sequence of costs? Shouldn't there be 2 cases where the cost is 1? For what value of n is the cost of Fibonacci(n) 4? – Scott Hunter Oct 15 '19 at 23:18
  • Your average is `O(2^n)`. Your best case is also `O(2^n)`. Technically you could say `O(1)`, but only for your hardcoded values, which are usually not discussed with big-o notation. That's like saying that bubble sort has a best-case of `O(1)`, because you've included a check for lists of length 0 and length 1. Yes technically that is true, but saying so doesn't really convey the information that a big-o analysis is supposed to convey. – mypetlion Oct 15 '19 at 23:18
  • @ScottHunter you are actually right. If I do include `n=1` and `n=2` into my calculations, it doesn't give me the result I have there. I guess it correlates with the comment by @mypetlion , who also suggested not to include base cases. I guess I used the geometric series because I already knew that the best case should be `O(2^n)` – Alex.Kh Oct 15 '19 at 23:27
  • The best case *isn't* O(2^n). – Scott Hunter Oct 15 '19 at 23:43
  • @ScottHunter I would still say that the best case is `O(1)` – Alex.Kh Oct 15 '19 at 23:44
  • @Alex.Kh Nope, not true. Best case, average case, worst case only applies to data dependent algorithms. For example, a quick sort might run in O(nlogn) time for one array, but run in O(n^2) time for a different array **of the same size**. In other words, the exact same value of `n` can result in very different running times. With the Fibonacci code you've shown, there is only one possible running time for each value of `n`. And that running time is O(2^n). – user3386109 Oct 15 '19 at 23:52
  • @ScottHunter Care to explain? – mypetlion Oct 15 '19 at 23:54
  • @user3386109 For example, let's talk about the best case scenario. If `n=1` , the function will simply perform 1 comparison and return the result. In any case, it would produce it for a linear time as it would not have to do anything else, including the recursion. So why would you say that it's always O(n^2)? The same is for the average case. Please explain me how you calculated it. – Alex.Kh Oct 16 '19 at 00:00
  • 1
    @Alex.Kh You're confusing **running time** and **time complexity**. Running time can be computed for a particular value of `n`. Time complexity is a **function** that provides an estimate of the running time for large values of `n`. When you say that something is O(1), you're saying the running time is constant, regardless of the value of `n`. – user3386109 Oct 16 '19 at 00:10
  • @user3386109. Just to be sure that I do understand it correctly, when you are talking about the **running time** , you mean O(n) , right? While the **time complexity** is T(n)? – Alex.Kh Oct 16 '19 at 00:13
  • 1
    @Alex.Kh No. O(some function) is the time complexity of an algorithm. T(n) is a common notation for a recurrence relation used when computing time complexity. Running time is the number of operations needed to compute a result for a particular value of `n`. – user3386109 Oct 16 '19 at 00:19
  • @user3386109 thank you for the explanation. I will look into it more thoroughly. I will also close the question down, as my original question received an answer. – Alex.Kh Oct 16 '19 at 00:22
  • @Alex.Kh Ok, best of luck :) – user3386109 Oct 16 '19 at 00:25

0 Answers0