A bit of background: I want to calculate the array factor of a MxN antenna array, which is given by the following equation:
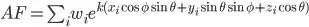 Where w_i are the complex weight of the i-th element, (x_i,y_i,z_i) is the position of the i-th element, k is the wave number, theta and phi are the elevation and azimuth respectively, and i ranges from 0 to MxN-1.
Where w_i are the complex weight of the i-th element, (x_i,y_i,z_i) is the position of the i-th element, k is the wave number, theta and phi are the elevation and azimuth respectively, and i ranges from 0 to MxN-1.
In the code I have:
-theta and phi are np.mgrid with shape (200,200) each,
-w_i, and (x,y,z)_i are np.array with shape (NxM,) each
so AF is a np.array with shape (200,200) (sum over i).There is no problem so far, and I can get AF easily doing:
af = zeros([theta.shape[0],phi.shape[0]])
for i in range(self.size[0]*self.size[1]):
af = af + ( w[i]*e**(-1j*(k * x_pos[i]*sin(theta)*cos(phi) + k * y_pos[i]* sin(theta)*sin(phi)+ k * z_pos[i] * cos(theta))) )
Now, each w_i depends on frequency, so AF too, and now I have w_i with shape (NxM,1000) (I have 1000 samples of each w_i in frequency). I tried to use the above code changing
af = zeros([1000,theta.shape[0],phi.shape[0]])
but I get 'operands could not be broadcast together'. I can solve this by using a for loop through the 1000 values, but it is slow and is a bit ugly. So, what is the correct way to do the summation, or the correct way to properly define w_i and AF ?
Any help would be appreciated. Thanks.
edit The code with the new dimension I'm trying to add is the next:
from numpy import *
class AntennaArray:
def __init__(self,f,asize=None,tipo=None,dx=None,dy=None):
self.Lambda = 299792458 / f
self.k = 2*pi/self.Lambda
self.size = asize
self.type = tipo
self._AF_DATA_SIZE = 200
self.theta,self.phi = mgrid[0 : pi : self._AF_DATA_SIZE*1j,0 : 2*pi : self._AF_DATA_SIZE*1j]
self.element_pos = None
self.element_amp = None
self.element_pha = None
if dx == None:
self.dx = self.Lambda/2
else:
self.dx = dx
if dy == None:
self.dy = self.Lambda/2
else:
self.dy = dy
self.generate_array()
def generate_array(self):
M = self.size[0]
N = self.size[1]
dx = self.dx
dy = self.dy
x_pos = arange(0,dx*N,dx)
y_pos = arange(0,dy*M,dy)
z_pos = 0
ele = zeros([N*M,3])
for i in range(M):
ele[i*N:(i+1)*N,0] = x_pos[:]
for i in range(M):
ele[i*N:(i+1)*N,1] = y_pos[i]
self.element_pos = ele
#self.array_factor = self.calculate_array_factor()
def calculate_array_factor(self):
theta,phi = self.theta,self.phi
k = self.k
x_pos = self.element_pos[:,0]
y_pos = self.element_pos[:,1]
z_pos = self.element_pos[:,2]
w = self.element_amp*exp(1j*self.element_pha)
if len(self.element_pha.shape) > 1:
#I have f_size samples of w_i(f)
f_size = self.element_pha.shape[1]
af = zeros([f_size,theta.shape[0],phi.shape[0]])
else:
#I only have w_i
af = zeros([theta.shape[0],phi.shape[0]])
for i in range(self.size[0]*self.size[1]):
**strong text**#This for loop does the summation over i
af = af + ( w[i]*e**(-1j*(k * x_pos[i]*sin(theta)*cos(phi) + k * y_pos[i]* sin(theta)*sin(phi)+ k * z_pos[i] * cos(theta))) )
return af
I tried to test it with the next main
from numpy import *
f_points = 10
M = 2
N = 2
a = AntennaArray(5.8e9,[M,N])
a.element_amp = ones([M*N,f_points])
a.element_pha = zeros([M*N,f_points])
af = a.calculate_array_factor()
But I get
ValueError: 'operands could not be broadcast together with shapes (10,) (200,200) '
Note that if I set
a.element_amp = ones([M*N])
a.element_pha = zeros([M*N])
This works well.
Thanks.