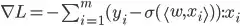Gradient for log regression loss

Question

I'm trying to write mini-batch gradient descent for log regression.

$\nabla L = - \sum_{i=1}^{m} (y_i - \sigma(\left<w,x_i\right>)):x_i$

Given numpy matrices X_batch (of shape (n_samples, n_features)) and y_batch (of shape (n_samples,)).

Naive way is to write loop:

def calc_loss_grad(self, X_batch, y_batch):
    n_samples, n_features = X_batch.shape
    loss_grad = np.zeros((n_features,))
    for i in range(n_samples):
        sigm = sigmoid(X_batch[i] @ self.weights)
        loss_grad += - (y_batch[i] - sigm) * X_batch[i]            
    return loss_grad

But seems like using loop is a bad idea w.r.t. speed. Any better ways? Pure numpy without a loop? Rewrite expression for gradient somehow?

How large are n_samples, n_features usually? weights has size n_features right? — max9111, Nov 08 '19 at 17:00
What makes you say that "using [a] loop is a bad idea w.r.t speed"? Is your problem that this code works fine, it just seems to run slow on your computer (In which case, this probably belongs on https://codereview.stackexchange.com)? Or are you running into fundamental complexity issues, where the loop seems to get slower and slower the more input elements you have? Or...? (basically: don't talk about what _seems_, talk about what _is_. What is the true problem that you're trying to solve?) — Mike 'Pomax' Kamermans, Nov 08 '19 at 17:37
@Mike It's running slower than it could. (compared to sklearn implementations at least). I'm thinking it's more of math problem, how to rewrite the expression in matrix form, so it could be coded in numpy operations only. — A.King, Nov 08 '19 at 18:07
Can you also provide the sklearn implementation for comparison? — max9111, Nov 08 '19 at 19:20

score 1 · Accepted Answer · answered Nov 08 '19 at 21:49

Note that this algorithm is memory bandwidth limited. If you optimize this in a larger context (real application) there is very likely a higher speedup possible.

Example

import numpy as np

#https://stackoverflow.com/a/29863846/4045774
def sigmoid(x):  
    return np.exp(-np.logaddexp(0, -x))

def calc_loss_grad_1(weights, X_batch, y_batch):
    n_samples, n_features = X_batch.shape
    loss_grad = np.zeros((n_features,))
    for i in range(n_samples):
        sigm = sigmoid(X_batch[i,:] @ weights)
        loss_grad += - (y_batch[i] - sigm) * X_batch[i]            
    return loss_grad

def calc_loss_grad_2(weights, X_batch, y_batch):
    sigm =-y_batch+sigmoid(X_batch@weights)          
    return sigm@X_batch

weights=np.random.rand(n_features)
X_batch=np.random.rand(n_samples,n_features)
y_batch=np.random.rand(n_samples)

#n_samples=int(1e5)
#n_features=int(1e4)
%timeit res=calc_loss_grad_1(weights, X_batch, y_batch)
#1.79 s ± 35.8 ms per loop (mean ± std. dev. of 7 runs, 1 loop each)
%timeit res=calc_loss_grad_2(weights, X_batch, y_batch)
#539 ms ± 21.9 ms per loop (mean ± std. dev. of 7 runs, 1 loop each)

#n_samples=int(1e3)
#n_features=int(1e2)
%timeit res=calc_loss_grad_1(weights, X_batch, y_batch)
#3.68 ms ± 44.7 µs per loop (mean ± std. dev. of 7 runs, 100 loops each)
%timeit res=calc_loss_grad_2(weights, X_batch, y_batch)
#49.1 µs ± 503 ns per loop (mean ± std. dev. of 7 runs, 10000 loops each)

Gradient for log regression loss

1 Answers1