filling a rectilinear polygon with rectangles

Question

Given a polygon, created entirely from rectangles, and defined by an array of points, where the edges are always aligned with the axis:

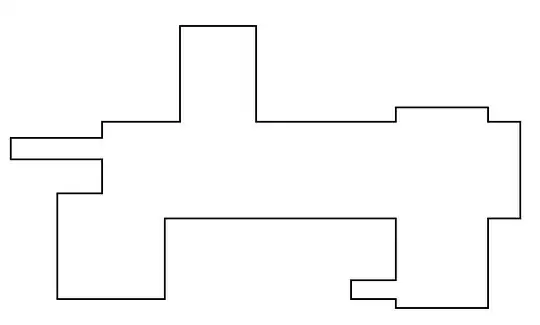
a polygon created entirely from intersecting rectangles

I am trying to determine a quick algorithm to find a small number of rectangles which can fill in this shape. This is something I did by hand to show the collection of rectangles I am describing: a polygon created entirely from intersecting rectangles filled with non-overlapping rectangles

EDIT: Here is some simple processing code to create this shape (well, close to it).

float[] xpts = {0,    50,  50,  100, 100, 150, 150, 250, 250, 300, 300, 325, 325, 300, 300, 250, 250, 210, 210, 250, 250, 125, 125, 25, 25,   50,  50,  0 };
float[] ypts = {100, 100,  80,   80, 10,   10,  80, 80,  75,  75, 80,   80,  200, 200, 300, 300, 275, 275, 260, 260, 200, 200, 270, 270, 165, 165, 125, 125};


void setup( )
{
  size( 350, 350 );
}

void draw( )
{

stroke( 0 );
strokeWeight( 1.5 );

float px = xpts[0];
float py = ypts[0];
for (int i=1; i < xpts.length; i++)
{
  float nx = xpts[i];
  float ny = ypts[i];
  line( px, py, nx, ny );


  px = xpts[i];
  py = ypts[i];
}
float nx = xpts[0];
float ny = ypts[0];

line( px, py, nx, ny );
}

Are the edges alway axis aligned? you could use scan lines to find the largest area easily if they are. — Flexo, May 03 '11 at 22:04
Yes, the edges are always axis aligned (I will update the post). Could you give more detail on the scan line approach? Thx. — jedierikb, May 03 '11 at 22:06
@finnw - I think this is sufficiently different from that question - here the input is an edge list. — Flexo, May 04 '11 at 08:36
See [Algorithm for finding the fewest rectangles to cover a set of rectangles](http://stackoverflow.com/questions/5919298/algorithm-for-finding-the-fewest-rectangles-to-cover-a-set-of-rectangles/6634668#6634668). — Gareth Rees, Jul 09 '11 at 12:32

ltjax · Accepted Answer · 2011-05-20T07:33:51.937

7

Build a KD-Tree using existing edges as the splitter planes and ignore regions that are completely outside of the polygon during recursion. The leaf nodes will then make up a rectangular decomposition.

Getting a good decomposition is simply a matter of which splitter to choose in each step of the recursion. You might wanna use a simple heuristic that halves the remaining area each step. If you want, you can also just try a few different splitters!

Here's some pseudo code:

function makeRects(Rect r, Polygon p)

  if p is empty
    if r is inside your original polygon
      add r to results

  else
    choose good splitter s

    makeRects(left part of r relative to s, left part of p relative to s)
    makeRects(right part of r relative to s, right part of p relative to s)

Splitters for the OPs sample decomposition

edited May 20 '11 at 07:33

answered May 06 '11 at 12:53

ltjax

15,837
3
39
62

2

Could you give an example? I am not really clear on how the children of each split are defined. – Null Set May 06 '11 at 16:52
Done - hope that helps. The children of each split are just the remaining subspaces. I.e. the two halves of the splitting plane intersected with the subspace associated of the parent node. – ltjax May 08 '11 at 16:15
2

Some pseudo code (could be very high level) would be helpful to understand how to operationalize your suggestion. Thx much. – jedierikb May 20 '11 at 03:31
Added some pseudo-code, as you requested. It leaves a lot of freedom tho. For example, you don't really need to explicitly test whether r is inside the original polygon to break the recursion: you can usually derive that from the splitter plane one level above! – ltjax May 20 '11 at 07:37
1

I get it. Thank you. But isn't "left part of p relative to s" a rather expensive operation? I understand it gets less expensive the more p is pruned, but it is still a lot of point checks, no? – jedierikb May 20 '11 at 18:25
It should be linear, if you implement it naively. But even then it should be pretty quick, so I wouldn't worry about it too much. – ltjax May 20 '11 at 19:31

score 1 · Answer 2 · answered May 04 '11 at 14:15

1

Sounds a lot like a NP problem to me. That means, there are certainly a couple of algorithms that can quickly fill your shape with rectangles, if the number of rectangles doesn't really matter to you, but if you insist on the smallest number, then you better forget about the word "quick". Actually you should even forget about the word "smallest" and instead use "small", since determining if the set is smallest could already be a huge problem for the algorithm.

answered May 04 '11 at 14:15

Mecki

125,244
33
244
253

Smallest changed to small. Thx! – jedierikb May 06 '11 at 12:44
can you sketch a proove why this is NP ? – citykid Jun 19 '14 at 12:24
1

@citykid Now that the question says small, it is not a NP problem any more, but originally it read smallest. Show me a mathematical test to verifies a solution is "smallest" and that runs in polynomial time. I don't know of any, thus verifying a solution is smallest is already a NP problem and thus finding the smallest solution is NP as well. It is similar to traveling salesman or knapsack problem - finding a good solution in short time is possible but finding the perfect solution is NP. – Mecki Jun 20 '14 at 16:36
well done, agreed, it is quite knapsack. – citykid Jun 20 '14 at 20:02
Hi, thanks for this question. I made the graph rectices and reduced it with hopcork and karp algorithm. You even may only shortcut this step by only draw cut lines just to transform the polygon (orthogon) in a set of rectangle. As a result you'll get may be more rectangles than the fewest acount of rectangles but it will often not be a big problem. Well if you treat thousands of small orthogons in a strange app may be. The problem now for me is that i cannot fill the rectangles once i have them drawned. I struggle to understand the proposed algorighm. Examples somewhere? thank's. – Jean-Yves DANIEL Apr 06 '21 at 16:09
Your assumption is false. See ["if a polygon has all its sides axis-parallel, it is possible to find a partition into the minimum possible number of rectangles in polynomial time"](https://mathoverflow.net/questions/28303/split-polygon-into-minimum-amount-of-rectangles-and-triangles/28350#28350) – arkon May 15 '22 at 11:30

filling a rectilinear polygon with rectangles

2 Answers2

Linked