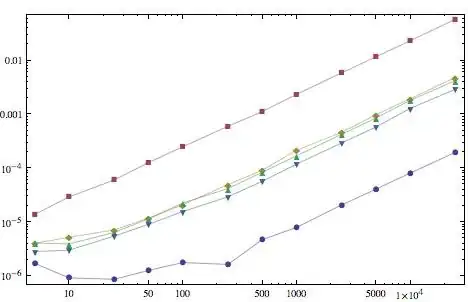
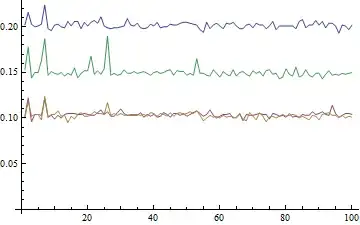
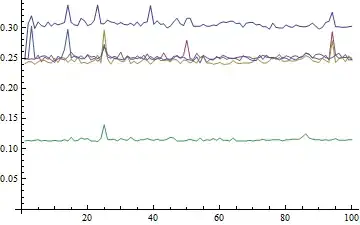
I think this is as fast as it gets, within Mathematica programming practices. The only way I see to attempt to make it faster within mma is to use Compile with the C compilation target, as follows:
getMinMax =
Compile[{{lst, _Real, 1}},
Module[{i = 1, min = 0., max = 0.},
For[i = 1, i <= Length[lst], i++,
If[min > lst[[i]], min = lst[[i]]];
If[max < lst[[i]], max = lst[[i]]];];
{min, max}], CompilationTarget -> "C", RuntimeOptions -> "Speed"]
However, even this seems to be somewhat slower than your code:
In[61]:= tst = RandomReal[{-10^7,10^7},10^6];
In[62]:= Do[getMinMax[tst],{100}]//Timing
Out[62]= {0.547,Null}
In[63]:= Do[{Min@#,Max@#}&[tst],{100}]//Timing
Out[63]= {0.484,Null}
You probably can write the function entirely in C, and then compile and load as dll - you may eliminate some overhead this way, but I doubt that you will win more than a few percents - not worth the effort IMO.
EDIT
It is interesting that you may significantly increase the speed of the compiled solution with manual common subexpression elimination (lst[[i]] here):
getMinMax =
Compile[{{lst, _Real, 1}},
Module[{i = 1, min = 0., max = 0., temp},
While[i <= Length[lst],
temp = lst[[i++]];
If[min > temp, min = temp];
If[max < temp, max = temp];];
{min, max}], CompilationTarget -> "C", RuntimeOptions -> "Speed"]
is a little faster than {Min@#,Max@#}.